Найти область определения. у=4х^2+2х-5
Определить четность или нечётность.
у=2х^3–4х
Найти точки пересечения графика функции с осями координат.
у=3х^3-6х
Найти критические точки.
у=х^4-8х^2
Найти промежутки возрастания и убывания.
у = 12х^2+14х
Найти точки экстремума и экстремум функции.
у=3х^3-6х
1) Пусть последовательность положительных чисел
является геометрической прогрессией, тогда
с формулы общего члена геометрической прогрессии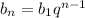
данную последовательность представим в виде:
2) Прологарифмируем по основанию
:
3) Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел.
. . . . . . . . . . . . . . . . . . . . . . . .
4) Рассмотрим полученную последовательность:
Очевидно, это арифметическая прогрессия, где
Доказано.
2. а) приведем к ОЗ=6, получим
9х-3х²+2х²-х-6х=0; -х²+2х=0; -х*(х-2)=0; х=0; х-2=0⇒х=2
ответ 0; 2.
б)ОДЗ у≠-2; у≠0; приведем к ОЗ=у*(у+2); у²+4у=2у²+4у-у-2; перенесем влево все члены, приведем подобные, получим у²-у-2=0, по теореме. обратной теореме Виета у=2; у=-1, оба корня входят в ОДЗ.
ответ 2; -1.
в) ОДЗ =≠-2; х≠3; приведем к общему знаменателю.
(5х-2)*(х-3)=(6х-21)*(х+2);
5х²-15х-2х+6=6х²+12х-21х-42; х²+8х-48=0; По Виету х=-12; х=4, оба корня входят в ОДЗ,
ответ х=-12; х=4.
3. Рассмотрим разность левой и правой частей. неравенство будет доказано, если эта разность будет больше нуля. итак.
а) х²+2х+1-(х²+2х)=х²-х²+2х-2х+1=1>0, доказано.
б) если докажем, что разность левой и правой частей неотрицательно, то неравенство будет доказано.
а²+1-2*(3а-4)=а²-6а+1+8=а²-6а+9=(а-3)²≥0.
Доказано.