Левая часть неравенства должна существовать, поэтому a + x >= 0, a - x >= 0
Переписываем систему в виде -a <= x <= a, |x| <= a откуда видно, что a >= 0. Можно сразу записать, что если a < 0, то решений нет.
Тогда обе части исходного неравенства неотрицательные, и можно возводить в квадрат. a + x + 2sqrt(a^2 - x^2) + a - x > a^2 sqrt(a^2 - x^2) > a(a - 2)/2
Если правая часть отрицательна, то решение неравенства - все значения, при которых корень существует. a(a - 2)/2 < 0 при 0 < a < 2, так что еще одна часть ответа такова: если 0 < a < 2, то -a <= x <= a.
Осталось рассмотреть случай, когда a(a - 2) >= 0. Тогда вновь можно возводить неравенство в квадрат. a^2 - x^2 > (a^4 - 4a^3 + 4a^2)/4 x^2 < a^3 (4 - a)/4.
У этого неравенства есть шанс иметь решения, если правая часть строго положительна, поэтому предпоследняя часть ответа: если a = 0 или a >= 4, решений нет. Осталось рассмотреть последний случай 2 <= a < 4.
Заметим, что при таких a правая часть меньше a^2, ведь a^3 (4 - a) / 4 / a^2 = a (4 - a) / 4 < 2 * (4 - 2) / 4 = 1 (известно, что квадратичная парабола a (4 - a) / 4 достигает максимального значения в вершине), поэтому все корни существуют, и последняя часть ответа: если 2 <= a < 4, то -sqrt(a^3 (4 - a))/2 < x < sqrt(a^3 (4 - a))/2.
Собираем всё в одно и получаем ответ. ответ. Если 0 < a < 2, то -a <= x <= a; если 2 <= a < 4, то -sqrt(a^3 (4 - a))/2 < x < sqrt(a^3 (4 - a))/2, для остальных a решений нет.
a + x >= 0,
a - x >= 0
Переписываем систему в виде
-a <= x <= a,
|x| <= a
откуда видно, что a >= 0.
Можно сразу записать, что если a < 0, то решений нет.
Тогда обе части исходного неравенства неотрицательные, и можно возводить в квадрат.
a + x + 2sqrt(a^2 - x^2) + a - x > a^2
sqrt(a^2 - x^2) > a(a - 2)/2
Если правая часть отрицательна, то решение неравенства - все значения, при которых корень существует.
a(a - 2)/2 < 0 при 0 < a < 2, так что еще одна часть ответа такова: если 0 < a < 2, то -a <= x <= a.
Осталось рассмотреть случай, когда a(a - 2) >= 0. Тогда вновь можно возводить неравенство в квадрат.
a^2 - x^2 > (a^4 - 4a^3 + 4a^2)/4
x^2 < a^3 (4 - a)/4.
У этого неравенства есть шанс иметь решения, если правая часть строго положительна, поэтому предпоследняя часть ответа: если a = 0 или a >= 4, решений нет. Осталось рассмотреть последний случай 2 <= a < 4.
Заметим, что при таких a правая часть меньше a^2, ведь
a^3 (4 - a) / 4 / a^2 = a (4 - a) / 4 < 2 * (4 - 2) / 4 = 1 (известно, что квадратичная парабола a (4 - a) / 4 достигает максимального значения в вершине), поэтому все корни существуют, и последняя часть ответа: если 2 <= a < 4, то -sqrt(a^3 (4 - a))/2 < x < sqrt(a^3 (4 - a))/2.
Собираем всё в одно и получаем ответ.
ответ. Если 0 < a < 2, то -a <= x <= a; если 2 <= a < 4, то -sqrt(a^3 (4 - a))/2 < x < sqrt(a^3 (4 - a))/2, для остальных a решений нет.
(см. объяснение)
Объяснение:
Самый верный решить любой параметр - это постараться построить его в координатах (b; x).
Попробуем применить этот прием здесь.
Сначала заметим, что при
равенство неверно при любом значении параметра. Тогда на протяжении решения при необходимости будем спокойно делить на 
.
Раскроем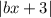
:
Видим гиперболу в координатах (b; x).
Построим ее и просчитаем знаки в областях, которые она образует, подставляя координаты соответствующих точек в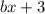
.
Тогда при
:
Строим фрагмент этого графика в определенных выше областях.
При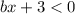
:
Тоже строим фрагмент этого графика в определенных выше областях.
Получим график уравнения:
(см. прикрепленный файл)
Итого:
ПриЗадание выполнено!