Характеристическое уравнение однородного диф. уравнения имеет вид:
Корни этого уравнения: k=-5 и k=-1, поэтому общее решение однородного уравнения y=
Найдем частное решение неоднородного уравнения в виде
u=
производная u=
вторая производная u=
Подставляя в исходное уравнение производные имеем систему уравнений: УРАВНЕНИЕ ПРИ СТЕПЕНИ имеет вид 5А-6А+А=0, 0А=0, верно при любом значении А.
Имеем:
Таким образом, общее решение исходного уравнения имеет вид:
Характеристическое уравнение однородного диф. уравнения имеет вид:
Найдем частное решение неоднородного уравнения в виде
u=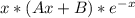
производная u=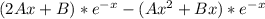
вторая производная u=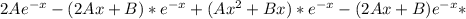
Подставляя в исходное уравнение производные имеем систему уравнений: УРАВНЕНИЕ ПРИ СТЕПЕНИ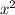 имеет вид 5А-6А+А=0, 0А=0, верно при любом значении А.
имеет вид 5А-6А+А=0, 0А=0, верно при любом значении А.
Имеем: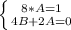
Таким образом, общее решение исходного уравнения имеет вид: