Объяснение:
У 6-му рядку помилково винесено з-під знака інтеграла 1/cos(х). А це зробити не можна , так як х залежить від t і так само від t залежить і 1/cos(х) .
Нельзя выносить за знак интеграла, т.к. там содержится переменная "х" ... Надо было выразить "х" через "t" и найти dx :
![(\frac{sec(x)6^{sin(x)}}{In(6)})` = \frac{1}{In(6)}(sec(x)6^{sin(x)})` = \frac{1}{In(6)}[(sec(x))`6^{sin(x)} + (6^{sin(x)})`sec(x)] =\\= \frac{1}{In(6)}[tg(x)sec(x)6^{sin(x)} + In(6)cos(x)6^{sin(x)}sec(x)] = = \frac{1}{In(6)}[\frac{6^{sin(x)}sin(x) }{cos^2(x)} + In(6)6^{sin(x)}] = \frac{6^{sin(x)}sin(x) + In(6)6^{sin(x)}cos^2(x) }{In(6)cos^2(x)} = = \frac{6^{sin(x)}sin(x)}{In(6)cos^2(x)} + 6^{sin(x)}](/tpl/images/4506/9654/de656.png)
Объяснение:
У 6-му рядку помилково винесено з-під знака інтеграла 1/cos(х). А це зробити не можна , так як х залежить від t і так само від t залежить і 1/cos(х) .
Нельзя выносить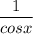
за знак интеграла, т.к. там содержится переменная "х" ... Надо было выразить "х" через "t" и найти dx :