Два числа называются равными по модулю N, если одно из них получено путем прибавления к другому (или вычитания от другого) некоторого количества раз числа N:
Свойство равенства по модулю:
Числа, равные по модулю N, дают при делении на N равные остатки.
Преобразуем первое слагаемое:
Преобразуем второе слагаемое:
Тогда:
Число , также как и равное ему по модулю 9 число 6, дает при делении на 9 остаток 6.
Два числа называются равными по модулю N, если одно из них получено путем прибавления к другому (или вычитания от другого) некоторого количества раз числа N:
Свойство равенства по модулю:
Числа, равные по модулю N, дают при делении на N равные остатки.
Преобразуем первое слагаемое:
Преобразуем второе слагаемое:
Тогда:
Число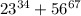 , также как и равное ему по модулю 9 число 6, дает при делении на 9 остаток 6.
, также как и равное ему по модулю 9 число 6, дает при делении на 9 остаток 6.
ответ: 6