Строим график и видим, что тут просто так не найти точки пересечения. Для нахождения точек пересечения решим кубическое уравнение
-x^3 + 3x^2 - 2 = 0
x1 = -0.732
x2 = 2.732
x3 = 1Сразу отбрасываем первый корень, получится, что площадь данной фигуры мы будем искать на промежутке [1;2.732]
S = ед^2
Строим график и видим, что тут просто так не найти точки пересечения. Для нахождения точек пересечения решим кубическое уравнение
-x^3 + 3x^2 - 2 = 0
x1 = -0.732
x2 = 2.732
x3 = 1
Сразу отбрасываем первый корень, получится, что площадь данной фигуры мы будем искать на промежутке [1;2.732]
S =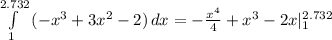
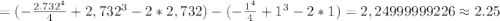 ед^2
ед^2