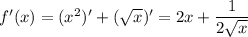найти приращение функции
f(x)=2x-1, x0=-1, дельта x=0,2

Выразим все через функции половинного аргумента
(2-a)*2sin(x/2)cos(x/2) + (2a+1)(cos^2(x/2)-sin^2(x/2)) < 25sin^2(x/2)+25cos^2(x/2)
(4-2a)sin(x/2)cos(x/2) + cos^{2}(x/2)(2a+1-25) + sin^{2}(x/2)(-2a-1-25) < 0
Делим все на cos^2(x/2)
(4-2a)*tg(x/2) + (2a-24) + (-2a-26)*tg^2(x/2) < 0
Делим все на -2, при этом меняется знак неравенства
(a+13)*tg^2(x/2) - (2-a)*tg(x/2) - (a-12) > 0
1) При а = -13 будет
-(2 + 13) tg(x/2) - (-13 - 12) > 0
-15 tg(x/2) +25 > 0
 15tg(x/2) < 25
tg(x/2) < 5/3
-pi/2 + pi*k < x/2 < arctg(5/3) + pi*k
x1 ∈ (-pi + 2pi*k; 2arctg(5/3) + 2pi*k)

2) При a=/= -13 будет квадратное неравенство относительно  tg(x/2)
Замена tg(x/2) = t
(a+13)*t^2 - (2-a)*t - (a-12) > 0
D = b^2 - 4ac = (2-a)^2 - 4(a+13)(-(a-12)) = 4 - 4a + a^2 + 4(a^2+a-156) =
= 5a^2 - 4*156 + 4 = 5a^2 - 620 = 5(a^2 - 124) = 5(a - √124)(a + √124)
При D = 0, то есть при a = -√124 и при а = √124 слева будет полный квадрат, который больше 0 при любых t, кроме
t = tg(x/2) =/= -b/(2a) = (2 - a)/(2a + 26)
x21 =/= 2arctg [(2 + √124)/(-2√124 + 26)] + 2pi*n
x22 =/= 2arctg [(2 - √124)/(2√124 + 26)] + 2pi*n
2 -  √124 < 0, а 26 - 2√124 > 0, поэтому x22 < x21
x2 ∈ (-pi + 2pi*n; x22) U (x22; x21) U (x21; pi + 2pi*n)

3) При D > 0, то есть при a < -√124 U a > √124 будет
t1 = tg(x/2) = (2-a - √(5a^2 - 620) ) / (2a + 26)
x31 = 2arctg [(2-a - √(5a^2 - 620) ) / (2a + 26)] + 2pi*m
t2 = tg(x/2) = (2-a + √(5a^2 - 620) ) / (2a + 26)
x32 = 2arctg [(2-a + √(5a^2 - 620) ) / (2a + 26)] + 2pi*m
x3 ∈ (-pi + 2pi*m; x31) U (x32; pi + 2pi*m)

4) При D < 0, то есть при -√124 < a < √124 будет вот что.
У уравнения слева корней нет, поэтому неравенство верно при любом t, 
то есть при всех x, при которых определен tg(x/2)
x4 ∈ (-pi + 2pi*h; pi + 2pi*h)

ответ: При  а = -13 x1 ∈ (-pi + 2pi*k; 2arctg(5/3) + 2pi*k)
При a = -√124 и при а = √124
x21 =/= 2arctg [(2 + √124)/(-2√124 + 26)] + 2pi*n
x22 =/= 2arctg [(2 - √124)/(2√124 + 26)] + 2pi*n
x2 ∈ (-pi + 2pi*n; x22) U (x22; x21) U (x21; pi + 2pi*n)
При a < -13 U -13 < a < -√124 U a > √124
x31 = 2arctg [(2-a - √(5a^2 - 620) ) / (2a + 26)] + 2pi*m
x32 = 2arctg [(2-a + √(5a^2 - 620) ) / (2a + 26)] + 2pi*m
x3 ∈ (-pi + 2pi*m; x31) U (x32; pi + 2pi*m)
При -√124 < a < √124
x4 ∈ (-pi + 2pi*h; pi + 2pi*h)

Очень непростое неравенство получилось.

1. Здесь в условии опечатка, скорее всего в точке x₀ = -1.

Прямая y=x-2 касается графика функции y=f(x) в точке x₀ = -1, то эта точка является общей для обеих функций, тогда f(-1) = -1-2=-3

ответ: -3.

2. Производная функции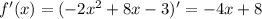

ответ: 16.

3.

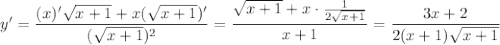
4. Производная функции: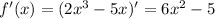

Используем геометрический смысл производной: f'(x₀) = tgα

ответ: 19.

5.

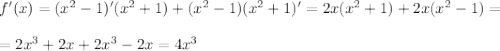
6.

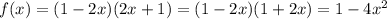
Производная функции: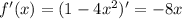 . Производная функции в точке 1, равна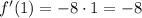

7. Производная функции: f'(x) = 1/2√x, ее значение в точке х=1 равна 1/2. Тогда касательная: y = f'(x0)(x-x0) + f(x0) = 1/2 * (x-1) + 1 = x/2 + 1/2

y(31) = 31/2 + 1/2 = 32/2 = 16

ответ: 16.

8.