Алгебра: Найти производную функции f(x)=2x^3-x^2 2x^3-x^2

Найти производную функции f(x)=2x^3-x^2 2x^3-x^2

Показать ответ

Ответ:

akikoaki

13.08.2022 23:46

$4^x - 14\cdot 2^x - 32 = 0\\\\(2^2)^x - 14\cdot 2^x - 32 = 0\\\\(2^x)^2 - 14\cdot 2^x - 32 = 0$

Введём замену: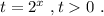 $t = 2^x\ , t0\ .$

t^2 - 14t - 32 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -32\\t_{1} + t_{2} = 14\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 16; t = -2}$ .

Но так как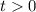 t 0 , то -2 не является решением этого уравнения. Выполняем обратную замену:

$2^x = 16\\2^x = 2^4\\\\\boxed{\textbf{x = 4}}$

ответ: 4.

$4^{x-3} = 32^x\\\\(2^2)^{x-3} = (2^5)^x\\\\2^{2(x-3)} = 2^{5x}\\\\2(x-3) = 5x\\\\2x - 6 - 5x = 0\\\\-3x = 6\\\\\boxed{\textbf{x = -2}}$

ответ: -2.

$5^{2x} - 4\cdot 5^x - 5 = 0\\\\(5^x)^2 - 4\cdot 5^x - 5 = 0$

Введём замену: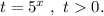 $t = 5^x\ ,\ t 0.$

t^2 - 4t - 5 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -5\\t_{1}+t_{2} = 4\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 5; t = -1}$

Но так как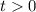 t 0 , то -1 не является решением этого уравнения. Выполняем обратную замену:

$5^x = 5\\\\\boxed{\textbf{x = 1}}$

ответ: 1.

$5^{x+2} + 11\cdot 5^x = 180\\\\5^x \cdot 5^2 + 11\cdot 5^x = 180\\\\5^x(25+11) = 180\\\\5^x\cdot 36 = 180\ \ \ \Big| :36\\\\5^x = 5\\\\\boxed{\textbf{x = 1}}$

ответ: 1.

$9^{\sqrt{x-5}} - 27 = 6\cdot 3^{\sqrt{x-5}}$

Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:

$x - 5 \geq 0\\x \geq 5$

Продолжаем решение:

$(3^2)^{\sqrt{x-5}} - 6\cdot 3^{\sqrt{x-5}} - 27 = 0\\\\(3^{\sqrt{x-5}})^2 - 6\cdot 3^{\sqrt{x-5}} - 27 = 0$

Введём замену: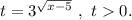 $t = 3^{\sqrt{x-5}}\ ,\ t0.$

t^2 - 6t - 27 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -27\\t_{1}+t_{2} = 6\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 9; t = -3}$

Но так как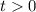 t 0 , то -3 не является решением этого уравнения. Выполняем обратную замену:

$3^{\sqrt{x-5}} = 9\\\\3^{\sqrt{x-5}} = 3^2\\\\\sqrt{x-5} = 2\\\\x - 5 = 4\\\\\boxed{\textbf{x = 9}}$

ответ: 9.

0,0(0 оценок)

Ответ:

ksyxa92

21.08.2022 08:01

ответ:Линейной функцией называется функция вида y = k * x + b, где x – независимая переменная, k и b – любые числа.

а) Рассмотрим функцию у = (4 * х – 7) : 2. Перепишем формулу данной функции в виде у = (4 * х) : 2 – 7 : 2 = 2 * х – 3,5. Ясно, что если принять k = 2 и b = –3,5, то получаем вид линейной функции из п. 1. Следовательно, данная функция является линейной функцией.

б) Рассмотрим функцию у = 3 * (х + 8). Перепишем формулу данной функции в виде у = 3 * х + 3 * 8 = 3 * х + 24. Ясно, что если принять k = 3 и b = 24, то получаем вид линейной функции из п. 1. Следовательно, данная функция является линейной функцией.

в) Рассмотрим функцию у = х * (6 – х). Перепишем формулу данной функции в виде у = х * 6 – х * х = 6 * х – х². Данная функция не является линейной функцией, так как в её составе наряду с линейным выражением (6 * х) имеется и нелинейное выражение (–х²).

г) Рассмотрим функцию у = х * (9 – х) + х². Перепишем формулу данной функции в виде у = х * 9 – х * х + х² = 9 * х. Ясно, что если принять k = 9 и b = 0, то получаем вид линейной функции из п. 1. Следовательно, данная функция является линейной функцией.

Объяснение:

0,0(0 оценок)

Популярные вопросы: Алгебра