По определению, производная есть предел отношения приращения функции к вызвавшему его приращению аргумента, при условии стремления этого приращения аргумента к нулю.
Для функции тангенса имеем:
Преобразуем разность тангенсов по формуле :
Рассмотрим предел произведения как произведение пределов:
Значение первого предела-сомножителя равно 1 (первый замечательный предел). Вычисляя второй предел-сомножитель, получим итоговый результат:
По определению, производная есть предел отношения приращения функции к вызвавшему его приращению аргумента, при условии стремления этого приращения аргумента к нулю.
Для функции тангенса имеем:
Преобразуем разность тангенсов по формуле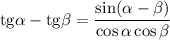 :
:
Рассмотрим предел произведения как произведение пределов:
Значение первого предела-сомножителя равно 1 (первый замечательный предел). Вычисляя второй предел-сомножитель, получим итоговый результат:
Таким образом: