В первом примере сгруппируем первые два члена и последние два, вынесем за скобки общий множитель, а потом еще раз применим формулу сокращенного умножения разность квадратов.
Во втором примере сгруппируем первый и последний члены, заметив и разложив по формуле сумма кубов, а во втором и третьем вынесем минус тэ за скобки, и опять, собрав все во вторых скобках приведем еще подобные.
В первом примере сгруппируем первые два члена и последние два, вынесем за скобки общий множитель, а потом еще раз применим формулу сокращенного умножения разность квадратов.
Во втором примере сгруппируем первый и последний члены, заметив и разложив по формуле сумма кубов, а во втором и третьем вынесем минус тэ за скобки, и опять, собрав все во вторых скобках приведем еще подобные.
1)к³-d²к-dк²+d³=(к³-d²к)+(-dк²+d³)=к(к²-d²)-d(к²-d²)=(к²-d²)(к-d)=
(к-d)(к+d)(к-d)=(к-d)²*(к+d)
2)0,001-0,1t-t²+t³=(0,001+t³)+(-0,1t-t²)=(0,1+t)(0,01-0,1t+t²)-t*(0,1+t)=
(0,1+t)*(0,01-0,1t+t²-t)=(0,1+t)(0,01-1,1t+t²)
ответ: a ∈ (-∞; -25/21) ∪ (1; 25/8).
Объяснение:
Заметим, что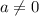
(т.к. при а = 0 данное уравнение преобразуется в линейный вид, что само собой имеет одно решение).
D = 25 - 8a
Квадратное уравнение имеет два различные корня, если D>0
25 - 8a > 0 ⇔ a < 25/8
Воспользуемся теоремой Виета:
Пусть 1/a = t, тогда получаем квадратное уравнение 25t² - 4t - 21 = 0
D = 16 + 2100 = 2116; √D = 46
t₁ = -0.84
t₂ = 1
Обратная замена:
1/a = -0.84 ⇔ a = -25/21
1/a = 1 ⇔ a=1
---------(-25/21)++++++++(0)+++++++++(1)------------
a ∈ (-∞; -25/21) ∪ (1;+∞)
С учетом существования корней, получим a ∈ (-∞; -25/21) ∪ (1; 25/8).