если ползуете функцей секанс :
------------------------------------------------------------------------------------------------------
если ползуете функцей секанс :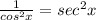
------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------