Объединим дроби:
Запишем в виде дроби со знаменателем 1:
Перемножим и :
Продифференцируем по правилу дифференцирования сложных функций, которое гласит, что равняется , где :
Дифференцируем.
Объединим дроби:
Запишем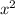
в виде дроби со знаменателем 1:
Перемножим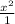
и 
:
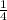Продифференцируем по правилу дифференцирования сложных функций, которое гласит, что![\frac{d}{dx} [f(g(x))]](/tpl/images/0927/1676/e2c84.png)
равняется 
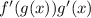, где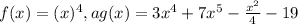 
:
Дифференцируем.