Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, , но сейчас это не нужно), нам повезло, это 32
Учитываем, что , получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
1. 32 және 17 сандарының көбейтіндісі санды өрнек түрінде жазыңдар.
А) 32 * 17 Б) 32: 17 С) 32 – 17 Д) 32 + 17
2. х пен 15 санының айырмасының мәнін табыңдар, х =20
А) 5 Б) 10 С) 15 Д) 20
3. 7у * 6 х коэффициенті неге тең?
А) 7 Б) 6 С) 15 Д) 1
4. 0; 2; 3; 5; 11; 13; 101; 102; 110, т. б. жұп сандардың қатарын анықта.
А) 0; 3; 5; Б) 0; 2; 11; 15; 101; С) 102; 101; 110; 0; 3; 5; Д) 2; 102; 110;
5. Сөйлемді аяқтаңдар.
« Егер, онда сан 2 – ге бөлінеді».
А) Жұп болса Б) тақ болса С) Жұп та, тақ та емес Д) дұрыс жауап жоқ
6. Сөйлемді аяқтаңдар.
« Егер, онда сан 9 - ға бөлінеді».
А) жұп болса Б) тақ болса С) цифрларының қосындысы 9 – ға бөлінеді
С) цифрларының қосындысы тақ болса
7. Бөлшектерді жазыңдар: алымы 3, бөлімі 7
А) Б) С) 3: 7 Д) 7: 3
8. 5 және 13 сандарының ең кіші еселігін табыңдар.
А) 45 Б) 35 С) 65 Д) 13
9. Теңдеу дегеніміз?
А) құрамында әрпі бар өрнек Б) құрамында саны бар өрнек С) құрамында әрпі де, саны да бар өрнек
10. Квадраттың ауданының формуласы.
А) S = a 2 b Б) S = ab С) S = 4a Д) S = a + b
11. Кубтың көлемін қалай анықтауға болады?
А) V = abc Б) V = a 3 С) V = a h Д) V = abh
12. Периметр дегеніміз?
А) Барлық қабырғалар көбейтіндісі Б) Барлық қабырғалар қосындысы
С) екі қабырғасының қосындысы Д) екі қабырғасының қосындысы
13. Үшбұрыш ауданы неге тең?
А) S = ab Б) S = a2 С) S = abc Д) S = (a + b) 2
14. Шеңбердің диаметрі неше радиусқа тең?
А) 1 Б) 3 С) 2 Д) 4
15. Радиус дегеніміз не?
А) Екі нүктенің ара қашықтығы Б) Центрдегі шеңбер бойындағы кез келген нүктемен қосатын кесінді.
С) Шеңбер бойындағы екі нүктені қосатын кесінді
16. Шеңбердің доғасы дегеніміз не?
А) екі нүктенің ара қашықтығы Б) центрді шеңбер бойындағы кез келген нүктемен қосады.
С) шеңбер бойындағы екі нүктені қосатын кесінді
17. Кез келген екі нүкте арқылы жүргізуге болады.
А) нүктелерді қосу керек Б) түзу С) кесінді Д) шеңбер
18. 1 метр 1 дециметр неше см артық?
А) 90 см Б) 9 см С) 900 см Д) 9000 см
19. Отбасында 7 қыз және әр қыздың бір – бірден бауыры бар. Отбасында барлығы неше бала бар? А) 7 Б) 8 С) 9 Д) 14
20. Ең кіші натурал сан?
А) 2 Б) 3 С) 0 Д) 1
21. Ең кіші жай сан?
А) 2 Б) 4 С) 0 Д) 6
22. Ең кіші үш таңбалы сан
А) 999 Б) 100 С) 101 Д) 105
23. Нәрселерді санау үшін қолданылатын сандар.
А) тақ сан Б) жұп сан С) натурал сан Д) бөлшек сан
24. 640 саны 5 – ке бөліне ме?
А) ия Б) жоқ С) екеуі де емес
25. Шеңбер бойындағы екі нүктені қосатын және центр арқылы өтетін кесінді.
А) диаметр Б) радиус С) доға Д) дұрыс жауап жоқ
Жауаптары:
1. А, 2. А, 3. С, 4. Д, 5. А, 6. С, 7. Б, 8. С, 9. А, 10. А, 11. Б, 12. Б, 13. С, 14. С, 15. Б,, 16. А, 17. Б, 18. А, 19. Б, 20. Д, 21. А, 22. Б, 23. С, 24. А, 25. А
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,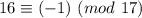
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что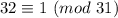
, получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.