Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
sashabibik777
22.10.2021 12:40 •
Алгебра
Найти q²z/qxqy для функции z=x-y/x+yв точку А (1,1)
Показать ответ
Ответ:
vovan2002vovap0181f
10.10.2021 14:10
d² z/ dxdy =
x =
Производная в точке А(1;1) равна:
ответ: 0
0,0
(0 оценок)
Популярные вопросы: Алгебра
Katia53535
06.12.2020 20:58
На материальную точку действует одновременно 2 силы f1 равно4н,f1 равно 3н определите велечину равнодействующие если угол между силами 270 градусов...
lolkekcheburek27
06.12.2020 20:58
Найдите корень уровнения 3(х-2)=х+4...
КеК5169
06.12.2020 20:58
Решите неравенство (3-3х) (х-2)(х+7) 0...
nastenadanil2698
06.12.2020 20:58
:(sinx+1/sinx)^2+(cosx+1/cosx)^2-tg^2x-ctg^2x...
plkg
06.12.2020 20:58
Знайти область визначення функції х+1: (х-5)(х+2)...
ruslankasaev
06.12.2020 20:58
Укожному купе вагону 4 місця.у якому купе їде пасажир,якщо він придбав квиток з номером місця 19?...
айлан8
06.12.2020 20:58
Впрогрессии четвертый член равен (-16),а первый член равен 2. найдите сумму первых шести членов прогрессии...
k1122
06.12.2020 20:58
Решить пару примеров cos a =5|3 и 3п|2 tg a= 15|8 и п...
настя06032005
18.08.2020 09:09
Сократите дробь: (4х^2-20x+25)/(2x^2+x-15)...
vladplotnikov2
18.08.2020 09:09
Выразите переменную x через y 2x-y=5...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
d² z/ dxdy = x =
x = 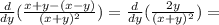
Производная в точке А(1;1) равна:
ответ: 0