По известной формуле распишем сумму m и n первых членов арифметической прогрессии:
Из условия получим следующее уравнение:
Или, раскрыв пропорцию, получим:
Так как получим:
ответ: 2.
Пусть D - разность прогрессии.
Тогда Sm = (1+1+D*(m-1))*m=(D*m-D+2)*m
Следовательно
(D*m-D+2)*m m^2 D*m-D+2 m
= , откуда =
(D*n-D+2)*n n^2 D*n-D+2 n
D*m*n-D*n+2*n=D*m*n-D*m+2*m
D*(m-n)=2*(m-n) . Поскольку m и n - разные числа, то D = 2
По известной формуле распишем сумму m и n первых членов арифметической прогрессии:
Из условия получим следующее уравнение:
Или, раскрыв пропорцию, получим:
Так как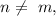 получим:
получим:
ответ: 2.
Пусть D - разность прогрессии.
Тогда Sm = (1+1+D*(m-1))*m=(D*m-D+2)*m
Следовательно
(D*m-D+2)*m m^2 D*m-D+2 m
= , откуда =
(D*n-D+2)*n n^2 D*n-D+2 n
D*m*n-D*n+2*n=D*m*n-D*m+2*m
D*(m-n)=2*(m-n) . Поскольку m и n - разные числа, то D = 2