Найти сумму бесконечно убывающей прогрессии
1) 6, 1, 1/;
2) -25, -5, -1,

Question

Алгебра: Найти сумму бесконечно убывающей прогрессии 1) 6, 1, 1/; 2) -25, -5, -1,

SonyaNexoda · Answer

Сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле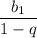 .Первая прогрессияНайдём знаменатель прогрессии:Теперь найдём сумму:Вторая прогрессия...