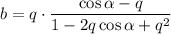, |q|<1
Пусть и - последовательности частичных сумм первого и второго, соответственного и b , a - их суммы.
По формуле Эйлера , мы получим
Здесь в этом случае бесконечно убывающая геометрическая прогрессия.
Преобразовывая в тригонометрическую форму по формуле Эйлера, мы получим
Откуда искомая сумма ряда
Пусть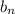 и
и 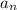 - последовательности частичных сумм первого и второго, соответственного и b , a - их суммы.
- последовательности частичных сумм первого и второго, соответственного и b , a - их суммы.
По формуле Эйлера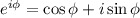 , мы получим
, мы получим
Здесь в этом случае бесконечно убывающая геометрическая прогрессия.
Преобразовывая в тригонометрическую форму по формуле Эйлера, мы получим
Откуда искомая сумма ряда