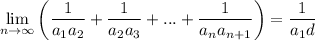Распишем сначала сумму для удобства и потом подсчитаем предел
Переходя к пределу при мы получим
ответ:
Распишем сначала сумму для удобства и потом подсчитаем предел
Переходя к пределу при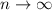 мы получим
мы получим
ответ: