Найти значение k для прямой пропорциональности, если известно, что график проходит через точку А (3; 18).​

Корень уравнения это такое число, что если его подставить вместо переменной, то получится верное равенство.

В задаче требуется проверить, какое из чисел является корнем уравнения, или никакое?

Подставим числа в уравнение.

Число 1: 3(1-7) + 4 = 7*1 - 1

3(-6) + 4 = 7 - 1

-18 + 4 = 6

Это неверно, значит, 1 не корень.

Число 0: 3(0-7) + 4 = 7*0 - 1

3(-7) + 4 = 0 - 1

-21 + 4 = - 1

Это неверно, значит, 0 не корень.

Число - 4: 3(-4-7) + 4 = 7(-4) - 1

3(-11) + 4 = - 28 - 1

-33 + 4 = - 29

Это верно, значит - 4 корень.

ответ: - 4

1)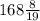 было у Бори;

2) 896(цветов) - было на празднике;

3) среднее арифметическое - 36

   мода ряда - 121

   размах ряда - 182

Объяснение:

1) Сейчас у Бори 160 руб(100%-95%).

160/0,95=16000/95=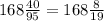 (руб) было у Бори.

2)100% -75%=25% георгинов было на празднике

224       25%

?             100%

(224*100)/25=224*4=896(цветов) - было на празднике.

3)

среднее арифметическое(сумма всех членов ряда, деленная на их количество) - (15+121-61+121+0+20)/6=36

мода ряда (число, которое в ряду встречается чаще других) - 121

размах ряда (разность наибольшего и наименьшего чисел) - 121-(-61)=182