Найти значение выражения: √(0,04 ×81)- 7√(1/49)
17 2) 0,8 3) 17 6/7 4) 4.
А2. Решить неравенство: 3(х - 2) – 5(х + 3) > х
(-∞; -7) 2) (- 7; +∞) 3) (-∞; 7) 4) (7; +∞)
А3. Периметр квадрата равен 20√2 см. Найти площадь этого квадрата.
200 см2 2) 25 см2 3) 100 см2 4) 50 см2
А4. Решить уравнение: у^2- 10у-39=0
-13; -3 2) 13; - 3 3) -13; 3 4) 13; 3
А5. Вершины треугольника АВС лежат на окружности, <А = 50˚, <В = 45˚. Чему равна градусная мера наименьшей из дуг АВ?
100˚ 2) 170˚ 3) 90˚ 4) 95˚
А6. Найти координаты вершины параболы у=х^2+ 4х+1
(3; 2) 2) (-1; -2) 3) (-2; -3) 4) (2; 1)
Часть 2.
В1. Вынести множитель из под знака корня: √(25х^2 у^5 ) при х < 0.
В2. Найти площадь равнобедренной трапеции с основаниями 10 см и 16 см и боковой стороной 5 см.
Часть 3.
С1. Мастер должен был изготовить 72 детали, а ученик 64 детали. Изготовляя в час на 4 детали больше, чем ученик, мастер выполнил заказ на 2 часа раньше. Сколько деталей в час изготовлял мастер и сколько ученик?
С2. Выберите верное утверждение.
1) В тупоугольном треугольнике все углы тупые
2) Биссектрисы треугольника пересекаются в центре его вписанной окружности
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны
4) Всякий равносторонний треугольник является остроугольным
В ответе укажите номера верных утверждений без пробелов, запятых и других дополнительных символов КЛАСС АЛГЕБРА
Пусть взято х частей первого сплава и у частей второго. В х частях первого сплава содержится частей первого металла и частей второго. В y частях второго сплава содержится частей первого металла и частей второго.
Главная
Положение о фестивале и конкурсах
Поиск по сайту
Подборка материалов ко Дню Конституции РФ
Подборка материалов ко Дню прав человека
Подборка материалов к 75 годовщине битвы за Москву 1941‒1942 гг.
Подборка материалов ко Дню волонтёра
Разделы
Конкурс «Презентация к уроку»
Конкурс по экологии «Земля — наш общий дом»
Конкурс «Электронный учебник на уроке»
Конкурс «Цифровой класс»
Конкурс «История регионов России»
Конкурс «Мы мир храним, пока мы помним о войне»
Астрономия
Биология
Начальная школа
География
Иностранные языки
Информатика
История и обществознание
Краеведение
Литература
Математика
Музыка
МХК и ИЗО
ОБЖ
ОРКСЭ
Русский язык
Руководство учебным проектом
Спорт в школе и здоровье детей
Технология
Физика
Химия
Экология
Экономика
Администрирование школы
Видеоурок
Внеклассная работа
Дополнительное образование
Инклюзивное образование
Классное руководство
Коррекционная педагогика
Логопедия
Мастер-класс
Общепедагогические технологии
Организация школьной библиотеки
Патриотическое воспитание
Профессия — педагог
Работа с дошкольниками
Работа с родителями
Социальная педагогика
Урок с использованием электронного учебника
Школьная психологическая служба
Решение задач на "сплавы", "смеси", "растворы"
Бескровных Татьяна Витальевна, учитель математики
Разделы: Математика
Задачи, связанные с понятием “концентрация” и “процентное содержание”, являются традиционно трудными для обучающихся. В них речь идет о сплавах, растворах и смесях, которые получаются при сплавлении или смешивании различных веществ. При решении таких задач принимаются некоторые допущения. Первое: если смешиваются два раствора, объем которых х и у, то получившаяся смесь будет иметь объем х + у. Второе: получившиеся смеси и сплавы имеют однородную консистенцию.
В смесях и растворах содержится некоторый объем чистого вещества. Отношение объема чистого вещества к объему всего раствора называется объемной концентрацией. (Содержание чистого вещества в единице объема). Концентрация, выраженная в процентах, называется процентным содержанием. При решении таких задач удобно пользоваться таблицей, которая понять задачу и по которой легче составить уравнение или систему. В работе приведены решения нескольких задач, а также предложены задачи для самостоятельного решения. Для удобства к задачам прилагаются ответы.
1. Некоторый сплав состоит из двух металлов, входящих в отношении 1 : 2, а другой содержит те же металлы в отношении 2 : 3. Из скольких частей обоих сплавов можно получить третий сплав, содержащий те же металлы в отношении 17 : 27?
Решение: Пусть взято х частей первого сплава и у частей второго. В х частях первого сплава содержится частей первого металла и частей второго. В y частях второго сплава содержится частей первого металла и частей второго.
Составим таблицу:
развернуть таблицу
В частях 1 металл 2 металл
1 сплав х частей частей частей
2 сплав у частей частей частей
3 сплав 44 части 17 частей 27 частей
развернуть таблицу
Из таблицы видно, что можно получить три уравнения. 1) х + у = 44 , 2)
3) . Решив систему из двух уравнений, получим
ответ: 9 частей первого сплава и 35 частей второго сплава.
Решим уравнение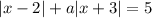 в зависимости от значений параметра (постоянной)
в зависимости от значений параметра (постоянной) 
Применим классическое решение уравнения типа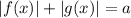
1) Найдем те значения , при которых обнуляются модули - это
, при которых обнуляются модули - это 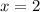 и
и 
2) Выставим на координатной оси эти значения:
эти значения:
3.1) Рассмотрим промежуток![x \in (-\infty; -3]](/tpl/images/1025/4528/6d9ac.png) :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули. Если подмодульное выражение меньше нуля, то для того чтобы его раскрыть, нужно изменить знак выражение, тем самым модуль раскроется с неотрицательным выражением.
Если , то
, то  , что верно при любых
, что верно при любых  из рассматриваемого промежутка
из рассматриваемого промежутка
Если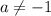 , то
, то 
3.2. Рассмотрим промежуток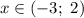 :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если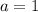 , то
, то  , что верно при любых
, что верно при любых  из рассматриваемого промежутка
из рассматриваемого промежутка
Если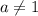 , то
, то 
Однако, 3 не входит в данный интервал, который мы рассматриваем.
3.3. Рассмотрим промежуток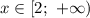 :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если , то
, то 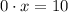 , что неверно ни при каких
, что неверно ни при каких 
Если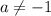 , то
, то 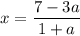
Рассмотрим данный ответ на заданном интервале. Этот ответ нам подойдет, если выполниться условие:
Решим данное неравенство методом интервалов:
1)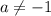
2)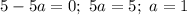
Отметим данные точки на координатной оси
Таким образом,![a \in (-1; \ 1]](/tpl/images/1025/4528/68d76.png)
Если