2. Найти нули производной: для этого приравнять производную к нулю и решить уравнение.
3. Построить числовую ось, отметить найденные точки и определить знаки производной на полученных интервалах.
1.
2.
3. На рисунке.
Как определены знаки на интервалах: берем произвольную точку из одного из интервалов, например на среднем, который от -4 до 2. На этом интервале лежит, например число 0. его и возьмем. Подставим в производную:
-24 < 0, значит на этом интервале функция убывает.
Такую же операцию проделываем и для двух других интервалов
Максимум - это точка в которой знак + меняется на знак -
-4
Объяснение:
Такие задачи решаем по схеме:
1. Найти производную функции.
2. Найти нули производной: для этого приравнять производную к нулю и решить уравнение.
3. Построить числовую ось, отметить найденные точки и определить знаки производной на полученных интервалах.
1.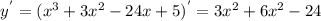
2.
3. На рисунке.
Как определены знаки на интервалах: берем произвольную точку из одного из интервалов, например на среднем, который от -4 до 2. На этом интервале лежит, например число 0. его и возьмем. Подставим в производную:
-24 < 0, значит на этом интервале функция убывает.
Такую же операцию проделываем и для двух других интервалов
Максимум - это точка в которой знак + меняется на знак -
Вывод: точка максимума равна -4
Объяснение:
Строим график функции f(x)=x²– 2x+3
x₀=-b/(2a)=2/2=1
y₀=1-2+3=2
Ветви направлены вверх.
х у
0 3
2 3
1) у=f(x)+1
Это означает, что график смещается на 1 вверх по оси ОУ.
Смещаем график. Значит вершина будет в точке (1; 3)
2) у = 3f(х);
Это означает, что график сжимается в 3 раза вдоль оси OX.
Вершина остается в той же точке х₀=1, а вот значение увеличится в 3 раза: у₀=2*3=6.
3) у = 3f(x) – 2
График, построенные в п. 2) смещаем на 2 вниз относительно оси ОУ.
При этом вершина окажется в точке (1; 4)