Не вычисляя корни x1 и x2 уравнения, найдите значения выражения. Используйте Виету
7-Д. 8-Е

ответ: Минимум (-3;-1). Рост функции на интервале (-3;+∞). Функция убывает на промежутке (-∞;-3)

Объяснение:

Наименьшее значение:

Перед нами уравнение параболы. Известно, что экстремальное значение параболы достигается при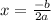 (здесь b - коэффициент при x, а а -  коэффициент при x^2)

Находим x:

x = -3 ⇒ подставляем это значение в функцию ⇒ y = -1 (данный y - минимум, которого может достичь функция)

Точка минимума - (-3;-1)

Промежуток, на котором функция возрастает:

Понятно, что данная парабола ветвями вверх, так как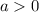 . Значит, функция возрастает после прохождения своего минимума:

Рост функции:

x ∈ (-3; +∞)

Промежуток на котором функция убывает:

Функция убывает пока не достигнет своего минимума

Уменьшение функции:

x ∈ (-∞; -3)

Для начала найдём, сколько слабо успевающих учеников.

1) 25-(10+3) = 12 - слабо успевающие

Наше событие(А) - это "не ниже 4", значит, оценка 4 или 5

Обозначим вероятности (P) того, что вызванный ученик окажется или отличником(У1), или ударником(У2), или слабо успевающим(У3).

P(У1) =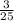

Р(У2) =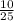

Р(У3) =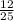

Вероятность того, что У1 ответит на оценку, не ниже 4 = 100%

Вероятность того, что У2 ответит на оценку, не ниже 4 = 100%, так как на экзамене он с равной долей вероятности получит или 4, или 5

Найдём Вероятность того, что У3 ответит на экзамене не ниже 4. С равной долей вероятности он может получить 3(О1) или 4(О2) или 5(О3). Вероятность получить одну из данных отметок равна 1/3.

P(O1)=P(O2)=P(O3)=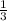

Благоприятному исходу соответствуют 2 случая: 4 или 5. Значит, вероятность получения одной из двух этих отметок равна

P(O2+O3)=P(O2)+P(O3)=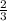

Вероятность события (А) =

P(A)=P(У1)*1+Р(У2)*1+P(У3)*P(O2+O3)= + +  * =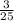

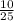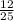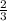0,12+0,4+0,32= 0,48

ответ: 0,48