Незнайка и кнопочка игральный кубик по одному - вопрос №8055655 от ParaDoksalS 26.04.2022 16:13

Question

Алгебра: Незнайка и кнопочка игральный кубик по одному разу. какова вероятность, что у незнайки будет большее количество очков? результат округлите до сотых.

ParaDoksalS · Answer

Вероятность того, что у Незнайки будет большее количество очков, равна вероятности благоприятствующих исходов (то есть, исходов, в которых действительно у Незнайки больше очков) ко всем [элементарным] исходам.

На таблице ниже (первое число означает количество очков Незнайки, а второе - количество очков Кнопочки) видно, что число благоприятствующих исходов (выделены красным) равно 15, а число всех исходов - 6² = 36.

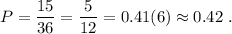
⇒ $P = \dfrac{15}{36} = \dfrac{5}{12} = 0.41(6) \approx 0.42 \; .$

Задача решена!

ответ: 0.42 .
Незнайка и кнопочка игральный кубик по одному разу. какова вероятность, что у незнайки будет большее