y(наиб) = 31 (в точке х = 2)
y(наим) = 5 (в точке x = 1)
На границах интервала.
Объяснение:
Для того, чтобы найти наибольшее и наименьшее значение функции нам необходимо:
Найти все стационарные точки.
Найти все критические точки.
Проверить границы интервала.
Данные точки ищутся с производной. Найдем производную данной функции:
x'(t) = 8 - 4.
Приравниваем производную к 0:
8 - 4 = 0
t = ± = ±- однако, эти точки не входят в наш интервал.
Таковых у нас нет, т.к. критические точки - это стационарные точки, но которые не входят в ОДЗ. (У нас ОДЗ от (-∞;∞+)).
Подставляем значения границ интервала и находим значения в этих точках:
x(1)=2*1^4−4*1+7 = 5
x(2)=2*2^4−4*2+7 = 31
Следовательно, это и есть наибольшее и наименьшее значение функции на заданном интервале.
Для вычисления корней 6x3 - 24x = 0 уравнения мы применим метод представления выражения в левой части уравнения в виде произведения.
И начнем мы с вынесения общего множителя.
Давайте прежде всего вынесем 6x за скобки и получим уравнение:
6x(x2 - 4) = 0;
Теперь мы можем применить ко второй скобке формулу сокращенного умножения:
n2 - m2 = (n - m)(n + m).
Итак, получаем уравнение:
6x(x - 2)(x + 2) = 0;
Произведение ноль, когда хотя бы один из множителей ноль.
1) 6x = 0;
x = 0;
2) x - 2 = 0;
x = 2;
3) x + 2 = 0;
x = -2.
ответ: 0; 2; -2.
2)25x³-10x²+x=0
x(25x-10x+1)=0
x(1)=0
25x-10x+1=0
(5x-1)²=0
5x-1=0
5x=1
x=1/5
__)
3)x³-4x²-9x+36=0
x²(x-4)-9(x-4)=0
(x²-9)(x-4)=0
x²-9=0 или x-4=0
x(1)=4
x²-9=0
(x-3)(x+3)=0
Или же(опять)
x²=9
x(2)=-3
x(3)=3
y(наиб) = 31 (в точке х = 2)
y(наим) = 5 (в точке x = 1)
На границах интервала.
Объяснение:
Для того, чтобы найти наибольшее и наименьшее значение функции нам необходимо:
Найти все стационарные точки.
Найти все критические точки.
Проверить границы интервала.
Пункт 1 - стационарные точки:Данные точки ищутся с производной. Найдем производную данной функции:
x'(t) = 8 - 4.
Приравниваем производную к 0:
8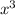
- 4 = 0
t = ±![\sqrt[3]{\frac{4}{3}}](/tpl/images/1201/1296/6cbb5.png)
= ±![\sqrt[3]{\frac{1}{2}}](/tpl/images/1201/1296/97e2a.png)
- однако, эти точки не входят в наш интервал.
Пункт 2 - критические точки:Таковых у нас нет, т.к. критические точки - это стационарные точки, но которые не входят в ОДЗ. (У нас ОДЗ от (-∞;∞+)).
Пункт 3 - границы графика:Подставляем значения границ интервала и находим значения в этих точках:
x(1)=2*1^4−4*1+7 = 5
x(2)=2*2^4−4*2+7 = 31
Следовательно, это и есть наибольшее и наименьшее значение функции на заданном интервале.
Для вычисления корней 6x3 - 24x = 0 уравнения мы применим метод представления выражения в левой части уравнения в виде произведения.
И начнем мы с вынесения общего множителя.
Давайте прежде всего вынесем 6x за скобки и получим уравнение:
6x(x2 - 4) = 0;
Теперь мы можем применить ко второй скобке формулу сокращенного умножения:
n2 - m2 = (n - m)(n + m).
Итак, получаем уравнение:
6x(x - 2)(x + 2) = 0;
Произведение ноль, когда хотя бы один из множителей ноль.
1) 6x = 0;
x = 0;
2) x - 2 = 0;
x = 2;
3) x + 2 = 0;
x = -2.
ответ: 0; 2; -2.
2)25x³-10x²+x=0
x(25x-10x+1)=0
x(1)=0
25x-10x+1=0
(5x-1)²=0
5x-1=0
5x=1
x=1/5
__)
3)x³-4x²-9x+36=0
x²(x-4)-9(x-4)=0
(x²-9)(x-4)=0
x²-9=0 или x-4=0
x(1)=4
x²-9=0
(x-3)(x+3)=0
Или же(опять)
x²=9
x(2)=-3
x(3)=3
Объяснение: