если известно, что искомая прямая y₁ = k₁x +b₁ параллельна прямой y=-4x+51 (у=кх +b), то мы знаем коэффициент k₁ = -4 при x, т.к. у параллельных прямых коэффициенты k и к₁ при х равны.
тогда мы уже имеем "половину" уравнения у₁ = -4х +b₁
теперь для определения b₁ используем то, что искомая прямая проходит через точку M(-1; 3). это означает, что координаты точки должны удовлетворять уравнению у₁ = -4х +b₁. подставим эти координаты
3= -4*(-1) +b₁ тогда b₁ = -1
и искомое уравнение
у₁ = -4х -1
теперь проверим, принадлежит ли построенному графику точка N(-50; 200). подставим ее координаты в уравнение у₁ = -4х -1
200 ≠ -4*(-50)-1
точка N(-50; 200) ∉ графику функции у₁ = -4х -1
тогда строим график по двум точкам
х = -1 у₁(-1) = 3 точка M(-1; 3)
х = 0 у₁(0) = -1
на первом фото построение по двум точкам у₁ = -4х -1 ║y=-4x+51
на втором показано, что точка N(-50; 200). ∉ графику у₁ = -4х -1
Поскольку эта задача уже решалась совсем недавно, позволю себе опустить подробности. Дважды возводя в квадрат (второй раз - уединяя корень), получим уравнение
Сначала будем искать так называемые парные корни, то есть корни вида Такие корни ходят парами, дают в разложении скобку (x²-a^2). Для поиска таких корней надо решать систему из двух уравнений, приравнивая отдельно к нулю сумму четных степеней и сумму нечетных степеней. Доказательство этого факта я оставляю читателю. В нашем случае находим корни Далее ищем кратные корни (они, как известно, ищутся из системы В результате находится кратный корень 2 кратности 2. После деления остается квадратный трехчлен с конями Работу по выделению истинных корней оставляю читателю. ответ:
На этом разрешите закончить это немного хулиганское решение.
Если кто-нибудь захочет услышать поподробнее про парные корни, составьте самостоятельно многочлен с парными корнями, приравняйте его к нулю и предложите мне решить такое уравнение. В этом случае я все внимание уделю этой теме.
Объяснение:
если известно, что искомая прямая y₁ = k₁x +b₁ параллельна прямой y=-4x+51 (у=кх +b), то мы знаем коэффициент k₁ = -4 при x, т.к. у параллельных прямых коэффициенты k и к₁ при х равны.
тогда мы уже имеем "половину" уравнения у₁ = -4х +b₁
теперь для определения b₁ используем то, что искомая прямая проходит через точку M(-1; 3). это означает, что координаты точки должны удовлетворять уравнению у₁ = -4х +b₁. подставим эти координаты
3= -4*(-1) +b₁ тогда b₁ = -1
и искомое уравнение
у₁ = -4х -1
теперь проверим, принадлежит ли построенному графику точка N(-50; 200). подставим ее координаты в уравнение у₁ = -4х -1
200 ≠ -4*(-50)-1
точка N(-50; 200) ∉ графику функции у₁ = -4х -1
тогда строим график по двум точкам
х = -1 у₁(-1) = 3 точка M(-1; 3)
х = 0 у₁(0) = -1
на первом фото построение по двум точкам у₁ = -4х -1 ║y=-4x+51
на втором показано, что точка N(-50; 200). ∉ графику у₁ = -4х -1
Поскольку эта задача уже решалась совсем недавно, позволю себе опустить подробности. Дважды возводя в квадрат (второй раз - уединяя корень), получим уравнение
Сначала будем искать так называемые парные корни, то есть корни вида
Такие корни ходят парами, дают в разложении скобку (x²-a^2). Для поиска таких корней надо решать систему из двух уравнений, приравнивая отдельно к нулю сумму четных степеней и сумму нечетных степеней. Доказательство этого факта я оставляю читателю. В нашем случае находим корни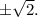 
Далее ищем кратные корни (они, как известно, ищутся из системы 
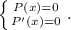В результате находится кратный корень 2 кратности 2. После деления остается квадратный трехчлен с конями 
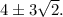Работу по выделению истинных корней оставляю читателю. ответ: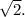 
На этом разрешите закончить это немного хулиганское решение.
Если кто-нибудь захочет услышать поподробнее про парные корни, составьте самостоятельно многочлен с парными корнями, приравняйте его к нулю и предложите мне решить такое уравнение. В этом случае я все внимание уделю этой теме.