Нужно Две меньшие стороны прямоугольной трапеции равны. Три различные стороны трапеции образуют арифметическую прогрессию. Периметр трапеции равен 144 м. Какая из сторон трапеции является наибольшей? Найди все стороны трапеции.
Теперь если поделить V₂ на V₁ (V₁ = × π × r² × h), то получим 0.847, в столько раз второй объем меньше чем первый, или же это можно записать как 100% - 84,7% = 15,3 %
ответ: x = arctg1/3 + πn ; x = π/4 + πn , nЄ Z .
Объяснение:
В умові сталася описка .
2cos²x + 4sinxcosx=3cos²x + 3sin²x ;
2cos²x + 4sinxcosx - 3cos²x - 3sin²x = 0 ;
- cos²x + 4sinxcosx - 3sin²x = 0 ; │: (- cos²x ≠ 0
3sin²x/cos²x - 4sinx/cosx + 1 = 0 ;
3tg²x - 4tgx + 1 = 0 ; заміна tgx = y ;
3y² - 4y + 1 = 0 ; D = 4 > 0 ; y₁ = 1/3 i y₂ = 1 .
повертаємось до змінної х :
tgx = 1/3 ; або tgx = 1 ;
x = arctg1/3 + πn , nЄ Z ; x = π/4 + πn , nЄ Z .
Второй объем меньше первого на 15,3 %
Объяснение:
Изначально радиус конуса r был 100%. Теперь же его увеличили на 10%, и теперь радиус конуса r₂ равен 110%. Так же это можно записать как:
r₂ = 1,1 × r
Теперь к высоте. С ней все тоже самое, только уменьшили. Значит h = 100%, a h₂ = 70%. То есть h₂ = 0,7 × h
Подставляем новые данные в формулу:
V₂ =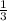
× π × (1,1 × r)² × 0,7 × h = 
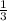× π × 1,21r² × 0,7h
Теперь если поделить V₂ на V₁ (V₁ =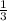
× π × r² × h), то получим 0.847, в столько раз второй объем меньше чем первый, или же это можно записать как 100% - 84,7% = 15,3 %