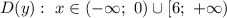Данная функция может существовать, если выполнится два условия (ОДЗ):
Решим по отдельности каждое условие:
Объединим эти два условия и получим:
ответ:
Данная функция может существовать, если выполнится два условия (ОДЗ):
Решим по отдельности каждое условие:
Объединим эти два условия и получим:
ответ: