Две прямые, первая из которых задается уравнением 10x-9y+a=0, а вторая задается уравнением 2x-y+b=0, проходят через точку B (2; 10). Пусть A-точка пересечения первой прямой с осью Oх, C- точка пересечения второй прямой с осью Oх. Найти площадь треугольника ABC.
1) Найти значение а в первом уравнении, чтобы найти уравнение первой функции:
10x - 9y + a = 0; B(2; 10);
а = 9у - 10х
а = 9*10 - 10*2
а = 90 - 20
а = 70;
Уравнение первой функции:
10x - 9y + 70 = 0
-9у = -10х - 70
9у = 10х + 70
у = (10х + 70)/9;
2) Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -7 -3 2
у 0 4,4 10
3) Найти координаты точки пересечения первой прямой с осью Ох.
Любой график пересекает ось Ох при у равном нулю.
у = (10х + 70)/9
(10х + 70)/9 = 0
10х + 70 = 0
10х = -70
х = -7.
Координаты точки пересечения первой прямой с осью Ох (-7; 0).
4) Найти значение b во втором уравнении, чтобы найти уравнение второй функции:
2x - y + b = 0; B(2; 10);
b = -2x + y
b = -2*2 + 10
b = 6;
Уравнение второй функции:
2x - y + 6 = 0
-у = -2х - 6
у = 2х + 6;
5) Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -1 0 1
у 4 6 8
6) Найти координаты точки пересечения второй прямой с осью Ох.
Любой график пересекает ось Ох при у равном нулю.
у = 2х + 6;
2х + 6 = 0
2х = -6
х = -3;
Координаты точки пересечения второй прямой с осью Ох (-3; 0).
#1
1) Сокращаем выражение на y3
2) Сокращаем выражение на x2
3) Сокращаем 25p и 15x на 5
ответ: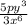
#2
1) Переворачиваем дробь (умножение вместо деления с переворотом дроби)
2) Сокращаем числа на 6
3) Сокращаем на m2
ответ :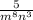
#3
1) Выносим 7 за общий множитель 7
2)Сократить дробь пользуясь группировкой a2-b2= (a-b)(a+b)
3) Сокращаем выражение на а4
4) Сокращаем на x+y
ответ :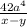
#4
1) Сократить дробь пользуясь группировкой a2-b2= (a-b)(a+b)
2) Вынести 4 за скобки
3)Переворачиваем дробь (умножение вместо деления с переворотом дроби)
4) Вынести 3 за скобки второй дроби
5) Сократить на a-3
6) Сократить на 2a+1
ответ :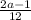
В решении.
Объяснение:
Две прямые, первая из которых задается уравнением 10x-9y+a=0, а вторая задается уравнением 2x-y+b=0, проходят через точку B (2; 10). Пусть A-точка пересечения первой прямой с осью Oх, C- точка пересечения второй прямой с осью Oх. Найти площадь треугольника ABC.
1) Найти значение а в первом уравнении, чтобы найти уравнение первой функции:
10x - 9y + a = 0; B(2; 10);
а = 9у - 10х
а = 9*10 - 10*2
а = 90 - 20
а = 70;
Уравнение первой функции:
10x - 9y + 70 = 0
-9у = -10х - 70
9у = 10х + 70
у = (10х + 70)/9;
2) Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -7 -3 2
у 0 4,4 10
3) Найти координаты точки пересечения первой прямой с осью Ох.
Любой график пересекает ось Ох при у равном нулю.
у = (10х + 70)/9
(10х + 70)/9 = 0
10х + 70 = 0
10х = -70
х = -7.
Координаты точки пересечения первой прямой с осью Ох (-7; 0).
4) Найти значение b во втором уравнении, чтобы найти уравнение второй функции:
2x - y + b = 0; B(2; 10);
b = -2x + y
b = -2*2 + 10
b = 6;
Уравнение второй функции:
2x - y + 6 = 0
-у = -2х - 6
у = 2х + 6;
5) Построить график. График линейной функции, прямая линия. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Таблица:
х -1 0 1
у 4 6 8
6) Найти координаты точки пересечения второй прямой с осью Ох.
Любой график пересекает ось Ох при у равном нулю.
у = 2х + 6;
2х + 6 = 0
2х = -6
х = -3;
Координаты точки пересечения второй прямой с осью Ох (-3; 0).
7) Найти длину основания треугольника АBC:
-3 - (-7) = -3 + 7 = 4 (ед.);
8) Найти площадь треугольника АBC:
S треугольника = 1/2 основания * h;
h = 10 (ед.);
S треугольника АBC = 1/2 * 4 * 10 = 20 (ед.²).