Выражения такого типа, когда в знаменателе сумма или разность числа и числа под корнем, избавляются от иррациональности простым методом. Вспоминаем формулу сокращенного умножения, разность квадратов:
. В нашем примере в знаменателе сумма, то есть из формулы. Нам нужно найти и умножить на это дробь, чтобы потом получилось , а , получится просто число, таким образом избавимся от корня в знаменателе. В нашем случае — это , — это . Соответственно, — это .
Важно отметить, что нужно умножить наше выражение не просто на , а на , потому что , а при умножении на 1 значение выражения не измениться. Если умножить просто на значение выражения поменяется.
Вот, собственно, и всё правило.
Ещё, после второго действия, второго =, была использована формула сокращённого умножения — разность кубов:
Два последних по списку выражения.
Объяснение:
1. (-1) в (-4) степени: отрицательное основание (-1) в четной степени будет положительным, а 1 в любой степени равен 1, так что 1
(-1) в (-3) степени: отрицательное основание (-1) в нечетной степени будет отрицательным, а 1 в любой степени равен 1, так что -1.
1 - (-1) = 1+1 = 2.
2. (-1) в 6 степени: -1 в четной степени будет просто 1, поскольку степень четная.
(-1) в 8 степени: то же самое, 1.
1+1=2.
3. (-1) в (-6) степени: отрицательное основание в четной степени положительно, значит просто 1.
(-1) в 8: было, 1.
1+1=2.
4. (-1) в 7: отрицательное основание в нечетной степени отрицательно, то есть -1.
1 в 7 степени: тут думаю все понятно, просто единица и просто в 7 степени, 1.
-1+1=0
5. (-1) в 4 степени: было подобное, 1.
(-1) в 9 степени: подобное тоже было, -1.
1+(-1)= 1-1 = 0.
Пояснение:
Выражения такого типа, когда в знаменателе сумма или разность числа и числа под корнем, избавляются от иррациональности простым методом. Вспоминаем формулу сокращенного умножения, разность квадратов:
Важно отметить, что нужно умножить наше выражение не просто на , а на
, а на 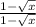 , потому что
, потому что  , а при умножении на 1 значение выражения не измениться. Если умножить просто на
, а при умножении на 1 значение выражения не измениться. Если умножить просто на  значение выражения поменяется.
значение выражения поменяется.
Вот, собственно, и всё правило.
Ещё, после второго действия, второго =, была использована формула сокращённого умножения — разность кубов: