Линейным углом двугранного угла называется угол, образованный лучами с вершиной на ребре, и при этом лучи лежат на гранях двугранного угла и перпендикулярны ребру.
В ∆ АВС опустим высоту АЕ перпендикулярно BC, тогда
DA перпендикулярен ( ABC )
AE принадлежит ( АВС )
Значит, DA перпендикулярен AE
AE перпендикулярен ВС
Тогда по теореме о трёх перпендикулярах DE перпендикулярен ВС
Из этого следует, что угол AED – линейный угол двугранного угла ABCD.
Рассмотрим ∆ АВС:
Высота равностороннего треугольника вычисляется по формуле:
h = a√3 / 2
где а – сторона равностороннего треугольника, h – высота
Сначала строим график функции . Это парабола с вершиной в точке О(0;0) , ветви вверх, проходит через точки (1;1) , (-1;1) , (2;4) , (-2;4) .Затем сдвигаем параболу вдоль оси ОХ на 3 единицы вправо, получим график функции .
А потом сдвигаем этот график вдоль оси ОУ вниз на 2 единицы , получим график функции . График нарисован красным цветом .
2)
Сначала строим график функции . Этот график проходит через точки (0;0) , (1;1) , (4;2) , .
Затем отображаем этот график относительно оси ОХ , получим график функции .
Потом сдвигаем этот график вдоль оси ОХ на 4 единицы вправо, получим график функции .
Этот график сдвигаем вдоль оси ОУ вниз на 1 единицу , получим график функции . График нарисован красным цветом .
Линейным углом двугранного угла называется угол, образованный лучами с вершиной на ребре, и при этом лучи лежат на гранях двугранного угла и перпендикулярны ребру.
В ∆ АВС опустим высоту АЕ перпендикулярно BC, тогда
DA перпендикулярен ( ABC )
AE принадлежит ( АВС )
Значит, DA перпендикулярен AE
AE перпендикулярен ВС
Тогда по теореме о трёх перпендикулярах DE перпендикулярен ВС
Из этого следует, что угол AED – линейный угол двугранного угла ABCD.
Рассмотрим ∆ АВС:
Высота равностороннего треугольника вычисляется по формуле:
h = a√3 / 2
где а – сторона равностороннего треугольника, h – высота
AE = AB × √3 / 2 = 6 × √3 / 2 = 3√3
Рассмотрим ∆ AED (угол DAE = 90°):
tg AED = AD / AE = 4 / 3√3 = 4√3 / 9
Объяснение:
Сначала строим график функции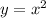 . Это парабола с вершиной в точке О(0;0) , ветви вверх, проходит через точки (1;1) , (-1;1) , (2;4) , (-2;4) .Затем сдвигаем параболу вдоль оси ОХ на 3 единицы вправо, получим график функции
. Это парабола с вершиной в точке О(0;0) , ветви вверх, проходит через точки (1;1) , (-1;1) , (2;4) , (-2;4) .Затем сдвигаем параболу вдоль оси ОХ на 3 единицы вправо, получим график функции 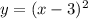 .
.
А потом сдвигаем этот график вдоль оси ОУ вниз на 2 единицы , получим график функции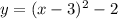 . График нарисован красным цветом .
. График нарисован красным цветом .
2)
Сначала строим график функции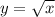 . Этот график проходит через точки (0;0) , (1;1) , (4;2) ,
. Этот график проходит через точки (0;0) , (1;1) , (4;2) , 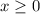 .
.
Затем отображаем этот график относительно оси ОХ , получим график функции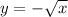 .
.
Потом сдвигаем этот график вдоль оси ОХ на 4 единицы вправо, получим график функции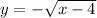 .
.
Этот график сдвигаем вдоль оси ОУ вниз на 1 единицу , получим график функции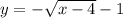 . График нарисован красным цветом .
. График нарисован красным цветом .