Алгебра: нужно представить 1 + Sin 2альфа в виде ( а + в )^2

нужно представить
1 + Sin 2альфа
в виде ( а + в )^2

Показать ответ

Ответ:

NuriEynullaeva

22.02.2021 02:12

Объяснение:

1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.

В примере в) коэффициенты k=5, значит их графики параллельны.

2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.

3. АБВГ

2413

4. 2x + y = 8

2x - y = 1

Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:

2x - (8 - 2x) = 1

2x - 8 + 2x = 1

4x = 9

x = 2,25

y = 8 - 2*2,25 = 8 - 4,5 = 3,5

ответ: (2,25; 3,5)

5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.

2)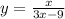 $y=\frac{x}{3x-9}$ . Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.

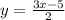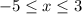
б) $y=\frac{3x-5}{2}$ при $-5\leq x\leq 3$

Если x = -5, то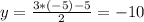 $y=\frac{3*(-5)-5}{2} =-10$

Если х= 3, то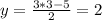 $y=\frac{3*3-5}{2} =2$

Значит,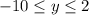 $-10\leq y\leq 2$

0,0(0 оценок)

Ответ:

7515575

27.04.2020 15:19

Первообразная (F(x)) - это функция (а не точка), которая ищется интегрированием другой функции (f(x))

Объяснение:

Находим интеграл от (3x-2)^8, для этого преобразовываем дифференциал (dx). добавляем 1/3 * 3 и тройку заносим под знак дифференциала: d(3x), 1/3 остаётся за интегралом. Константу можно добавить "просто так", ведь производная простого числа - 0, и получаем d(3x-2). Далее интегрируем это выражение как одну переменную: интеграл от а равен а^2/2. здесь интеграл от а^8 = а^9/9. Получаем ответ, не забываем С