нужно решение Первое, решила нужно второе и третье
Второе, упростить выражение
Третье, розвязать уровнение

Question

Алгебра: нужно решение Первое, решила нужно второе и третье Второе, упростить выражение Третье, розвязать уровнение

bbll1998 · Answer

ответ: 5 деталей за час сделает второй рабочий

Объяснение: пусть первый тратит x-часов на изготовление 72 деталей ; тогда второй тратит x+1 -часов на изготовление 50 тогда скорость первого рабочего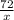 $\frac{72}{x}$ д/ч (деталей в час ) ; второго 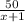$\frac{50}{x+1}$ д/ч и нам известно что первый рабочий за час делает на 3 детали больше, чем второй то есть 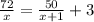$\frac{72}{x} =\frac{50}{x+1} +3$ решим уравнение 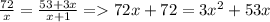$\frac{72}{x} =\frac{53+3x}{x+1} =72x+72=3x^2+53x$ дальше выйдет квадратное уравнение 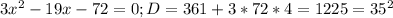3x^2-19x-72=0 ; D=361+3*72*4=1225=35^2 выйдут корни 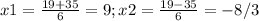$x1=\frac{19+35}{6} =9 ; x2=\frac{19-35}{6} =-8/3$ второй корень отрицательный поэтому не берем тогда тогда второй рабочий за час изготовит 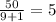$\frac{50}{9+1} =5$ деталей