Весь объем работы (задание) = 1 Время , требуемое для выполнения работы самостоятельно: I комбайн х ч. II комбайн (х+5) ч. Производительность труда при работе самостоятельно: I комбайн 1/х объема работы в час II комбайн 1/(х+5) об.р./час Производительность труда при совместной работе: 1/х + 1/(х+5) = (х+5+х)/ х(х+5) = (2х+5)/(х² +5х) об.р./час Время работы совместно = 6 часов. Уравнение. 6 * [ (2х+5)/(х² +5х) )] = 1 x² +5x ≠ 0 ⇒ x≠0 ; х≠ -5 (2х +5) /(х² + 5х) = 1/6 1(х² +5х) = 6(2х +5) х² +5х = 12х + 30 х² + 5х - 12х - 30 = 0 x² - 7x - 30 = 0 D=(-7)² - 4*1*(-30) = 49 + 120= 169 = 13² D>0 два корня уравнения х₁= (7 - 13) /(2*1) = -6/2=-3 - не удовлетворяет условию задачи х₂ = (7+13)/2 = 20/2 = 10 (ч.) время , требуемое I комбайну , для выполнение объема работы самостоятельно.
Проверим: 10 + 5 = 15 (ч.) потребуется II комбайну для выполнения задания самостоятельно 6 * (1/10 + 1/15 ) = 6 * [ (3+2)/30 ] = 6 * 1/6 = 1 - всё задание выполнено за 6 часов.
ответ: за 10 часов может выполнить задание первый комбайн, работая один.
Уфф, сегодня такую же на к/р не сделал =(
Вообщем чертишь табличку:
работа, производительность, время
1-ый комбайн 1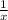 x
x
2-ой к. 1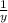 y
y
Вместе 1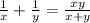
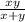
Пусть t1-x и t2=y, О.Д.З. : x>y, x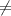 0, y
0, y 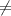 0
0
О.Д.З. : 2x-5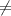 0
0
2x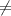 5
5
x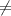 2.5
2.5
x=15 или x=2
Первое не подходит по О.Д.З.
ответ:15 и 10 часов.
Время , требуемое для выполнения работы самостоятельно:
I комбайн х ч.
II комбайн (х+5) ч.
Производительность труда при работе самостоятельно:
I комбайн 1/х объема работы в час
II комбайн 1/(х+5) об.р./час
Производительность труда при совместной работе:
1/х + 1/(х+5) = (х+5+х)/ х(х+5) = (2х+5)/(х² +5х) об.р./час
Время работы совместно = 6 часов.
Уравнение.
6 * [ (2х+5)/(х² +5х) )] = 1
x² +5x ≠ 0 ⇒ x≠0 ; х≠ -5
(2х +5) /(х² + 5х) = 1/6
1(х² +5х) = 6(2х +5)
х² +5х = 12х + 30
х² + 5х - 12х - 30 = 0
x² - 7x - 30 = 0
D=(-7)² - 4*1*(-30) = 49 + 120= 169 = 13²
D>0 два корня уравнения
х₁= (7 - 13) /(2*1) = -6/2=-3 - не удовлетворяет условию задачи
х₂ = (7+13)/2 = 20/2 = 10 (ч.) время , требуемое I комбайну , для выполнение объема работы самостоятельно.
Проверим:
10 + 5 = 15 (ч.) потребуется II комбайну для выполнения задания самостоятельно
6 * (1/10 + 1/15 ) = 6 * [ (3+2)/30 ] = 6 * 1/6 = 1 - всё задание выполнено за 6 часов.
ответ: за 10 часов может выполнить задание первый комбайн, работая один.