Сначала построим графики обеих функций: параболы и обычной прямой (чертеж смотрите ниже). Точками пересечения будут являться и (для того, чтобы их найти, просто решим квадратное уравнение или же теоремой Виета).
Чтобы найти искомую площадь, мы найдем площадь под графиком (выделено светло-голубым и желтым цветом) и площадь обведенной серым трапеции. После из второго вычтем первое и получим то, что нам нужно.
1). Площадь трапеции.
2). Площадь под графиком.
Нам понадобится следующая формула (Ньютона-Лейбница):
Умножить первое неравенство на 12, второе на 6, чтобы избавиться от дроби:
4х+3х<84
6-x>0
Первое неравенство:
7x<84
x<12
х∈(-∞, 12) интервал решений первого неравенства.
Неравенство строгое, скобки круглые.
Второе неравенство:
6-x>0
-x> -6
x<6 знак меняется
х∈(-∞, 6) интервал решений второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения 6, 12.
Штриховка по первому неравенству от 12 влево до - бесконечности.
По второму неравенству штриховка от 6 влево до - бесконечности.
Пересечение х∈ (-∞, 6), это и есть решение системы неравенств.
б)(3х-1)/2 -х<=2
2x-x/3>=1
Умножить первое неравенство на 2, второе на 3, чтобы избавиться от дроби:
3х-1-2х<=4
6x-x>=3
Первое неравенство:
х-1<=4
х<=5
х∈ (-∞, 5] интервал решений первого неравенства.
Неравенство нестрогое, скобка квадратная.
Второе неравенство:
5x>=3
x>=3/5
x>=0,6
х∈[0,6, +∞) интервал решений второго неравенства.
Неравенство нестрогое, скобка квадратная.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения 0,6, 5.
Штриховка по первому неравенству от 5 влево до - бесконечности.
По второму неравенству штриховка от 0,6 вправо до +бесконечности.
Пересечение х∈ [0,6, 5], это и есть решение системы неравенств.
Сначала построим графики обеих функций: параболы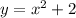
и обычной прямой 
(чертеж смотрите ниже). Точками пересечения будут являться 
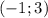и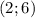 
(для того, чтобы их найти, просто решим квадратное уравнение 
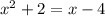или же 
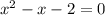теоремой Виета).
Чтобы найти искомую площадь, мы найдем площадь под графиком (выделено светло-голубым и желтым цветом) и площадь обведенной серым трапеции. После из второго вычтем первое и получим то, что нам нужно.1). Площадь трапеции.
2). Площадь под графиком.
Нам понадобится следующая формула (Ньютона-Лейбница):
Мы будем искать площадь на отрезке![[-1;2]](/tpl/images/1340/8031/7696d.png)
:
3). Разность - искомая площадь.
Задача решена!
а)х∈ (-∞, 6);
б)х∈ [0,6, 5].
Объяснение:
Решить систему неравенств:
а)х/3+х/4<7
1-x/6>0
Умножить первое неравенство на 12, второе на 6, чтобы избавиться от дроби:
4х+3х<84
6-x>0
Первое неравенство:
7x<84
x<12
х∈(-∞, 12) интервал решений первого неравенства.
Неравенство строгое, скобки круглые.
Второе неравенство:
6-x>0
-x> -6
x<6 знак меняется
х∈(-∞, 6) интервал решений второго неравенства.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения 6, 12.
Штриховка по первому неравенству от 12 влево до - бесконечности.
По второму неравенству штриховка от 6 влево до - бесконечности.
Пересечение х∈ (-∞, 6), это и есть решение системы неравенств.
б)(3х-1)/2 -х<=2
2x-x/3>=1
Умножить первое неравенство на 2, второе на 3, чтобы избавиться от дроби:
3х-1-2х<=4
6x-x>=3
Первое неравенство:
х-1<=4
х<=5
х∈ (-∞, 5] интервал решений первого неравенства.
Неравенство нестрогое, скобка квадратная.
Второе неравенство:
5x>=3
x>=3/5
x>=0,6
х∈[0,6, +∞) интервал решений второго неравенства.
Неравенство нестрогое, скобка квадратная.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения 0,6, 5.
Штриховка по первому неравенству от 5 влево до - бесконечности.
По второму неравенству штриховка от 0,6 вправо до +бесконечности.
Пересечение х∈ [0,6, 5], это и есть решение системы неравенств.