X км/ч - скорость лодки в стоячей воде х+2 - скорость лодки по течению х-2 - скорость лодки против течения 35/x+2 -время движения по течению 35/х-2 - время движения против течения 35/x+2 + 35/x-2 =6 переносим всё в левую часть, приводим к общему знаменателю: в числителе 35(x-2)+35(x-2)-6(x-2)(x+2), в знаменателе (x-2)(x+2) дробь =0 когда числитель =0, а знаменатель нет 35(x-2)+35(x+2)-6(x-2)(x+2)=0 70x-6x^2+24=0 3x^2-35x-12=0 D=35^2-4*3*(-12)=1369 x1=35-37/6=-1/3 не подходит x2=35+37/6=12 скорость лодки в стоячей воде 12км/ч
х+2 - скорость лодки по течению
х-2 - скорость лодки против течения
35/x+2 -время движения по течению
35/х-2 - время движения против течения
35/x+2 + 35/x-2 =6 переносим всё в левую часть, приводим к общему знаменателю: в числителе 35(x-2)+35(x-2)-6(x-2)(x+2), в знаменателе (x-2)(x+2)
дробь =0 когда числитель =0, а знаменатель нет
35(x-2)+35(x+2)-6(x-2)(x+2)=0
70x-6x^2+24=0
3x^2-35x-12=0
D=35^2-4*3*(-12)=1369
x1=35-37/6=-1/3 не подходит
x2=35+37/6=12 скорость лодки в стоячей воде 12км/ч
Объяснение:
1) А(-π/2 ; -1).
Здесь х= - π/2;
Для определения принадлежит ли точка А графику функции y=cos x
подставим значение х= - π/2, в формулу данной ф-ции:
y=cos x = cos (-π/2) =0. Итак при х= -π/2 , значение ф-ции у=0, а
это значит что точка А(-π/2;-1) не принадлежит графику функции
y=cos x.
2) B(9π/4; √2/2).
Объяснение аналогично варианту 1).
x= 9π/4;
Подставляем значения х в формулу данной функции:
y=cos x= cos(9π/4) = cos(2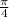 ) =cos(π/4 + 2π)= cos(π/4)= √2/2;
) =cos(π/4 + 2π)= cos(π/4)= √2/2;
При х =9π/4, значение функции у=√2/2, то точка В(9π/4; √2/2)
принадлежит графику функции y=cos x.
3) C(-4π;-1).
x=-4π; y=cos x= cos(-4π)=cos(-2π-2π)=cos(-2π)=cos(2π)=1;
При х= -4π, у=1.
Точка В(-4π;-1) не принадлежит графику функции y=cos x.