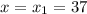1) Находим, за сколько дней уберет поле вторая бригада:
X= 12•75/100 = 9 дней
2) Находим, сколько сделала вторая бригада за 5 дней:
Х = 5•100/12 = 41,67%
3) Находим, сколько осталось убрать (в процентах):
100 – 41,67 = 58,33%
4) Находим, сколько процентов поля может убрать первая бригада за 1 день:
Х = 100/12 =8,33%
5) Находим, сколько процентов поля может убрать вторая бригада за 1 день:
Х = 100/9 = 11,11%
6) Считаем, сколько дней бригады вместе работали (n– берем, как количество дней):
58,33 = (8,33+11,11) • n
n = 58,33/19,44
n = 3 дня
Примечание:
100/9, 100/12, и тд. – писать дробью.
ОДЗ нашего уравнение:
Преобразуем левую часть уравнения, используя тождество:
-----(1)
В нашем случае , ,
Поэтому ------(2)
Правую часть нашего уравнения также преобразуем с тождества (1), предварительно представив слагаемое 3 в виде :
------(3)
C учетом (2) и (3) исходное уравнение примет вид:
-----(4)
Отсюда по свойству логарифма получим алгебраическое уравнение:
, или раскрывая скобки, получим
, или приведя подобные получим квадратное уравнение относительно :
Найдем его дискриминант:
Поскольку дискриминант положителен, то квадратное уравнение имеет два различных действительных корня:
удовлетворяет ОДЗ
не удовлетворяет ОДЗ.
Таким образом, только один корень квадратного уравнения является корнем исходного уравнения:
1) Находим, за сколько дней уберет поле вторая бригада:
X= 12•75/100 = 9 дней
2) Находим, сколько сделала вторая бригада за 5 дней:
Х = 5•100/12 = 41,67%
3) Находим, сколько осталось убрать (в процентах):
100 – 41,67 = 58,33%
4) Находим, сколько процентов поля может убрать первая бригада за 1 день:
Х = 100/12 =8,33%
5) Находим, сколько процентов поля может убрать вторая бригада за 1 день:
Х = 100/9 = 11,11%
6) Считаем, сколько дней бригады вместе работали (n– берем, как количество дней):
58,33 = (8,33+11,11) • n
n = 58,33/19,44
n = 3 дня
Примечание:
100/9, 100/12, и тд. – писать дробью.
ОДЗ нашего уравнение:
Преобразуем левую часть уравнения, используя тождество:
В нашем случае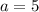 ,
, 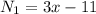 ,
, 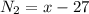
Поэтому![log_{5}(3x-11)+log_{5}(x-27)=log_{5}[(3x-11)(x-27)]](/tpl/images/0043/5175/0c853.png) ------(2)
------(2)
Правую часть нашего уравнения также преобразуем с тождества (1), предварительно представив слагаемое 3 в виде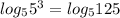 :
:
C учетом (2) и (3) исходное уравнение примет вид:
Отсюда по свойству логарифма получим алгебраическое уравнение:
Найдем его дискриминант: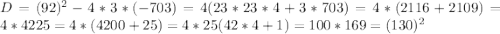
Поскольку дискриминант положителен, то квадратное уравнение имеет два различных действительных корня:
Таким образом, только один корень квадратного уравнения является корнем исходного уравнения: