(x-a)(x²-10x+9)=0 (x-a)(x-1)(x-9)=0 x₁=a; x₂=1; x₃=9 - корни уравнения составим из полученных корней все возможные последовательности: 1) 1, 9, а 2) 1, а, 9 3) а, 1, 9 4) а, 9, 1 5) 9, а, 1 6) 9, 1, а получено 6 последовательностей. убираем убывающие (4), (5), (6). получили три возрастающих последовательности. известно, что это арифметические прогрессии. находим значение а в каждой из них: 1) 1, 9, а d=9-1=8 => a=9+8=17 2) 1, a, 9 a=(1+9)/2=10/2=5 3) a, 1, 9 d=9-1=8 a=1-8=-7 итак, а равны 17, 5 и -7 x²-10x+9=0 корни уравнения находим по теореме виета: x₁*x₂=9 и x₁+x₂=10 => x₁=1, x₂=9 (x₁< x₂)
Доказать тождество:
1. Определим область допустимых значений.
1.1. Выражение слева имеет смысл, если его знаменатель не равен нулю:
1.2. Используя формулу приведения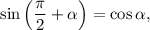 получаем:
получаем:
1.3. Умножим обе части на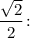
1.4. Поскольку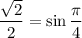 и
и 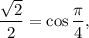 то получаем:
то получаем:
1.5. Используя формулу синуса суммы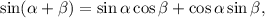 получаем:
получаем:
1.6. Так как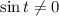 для
для 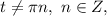 то:
то:
1.7. Перенесём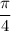 в правую часть, изменив знак на противоположный:
в правую часть, изменив знак на противоположный:
2. Докажем данное тождество, работая с левой частью равенства.
2.1. Преобразуем данное выражение, применив формулу косинуса двойного угла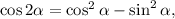 синуса двойного угла
синуса двойного угла 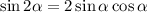 и формулу приведения
и формулу приведения 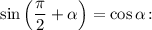
2.2. Замечаем в числителе следствие из основного тригонометрического тождества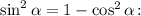
2.3. Вынесем в числителе общий множитель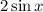 за скобки:
за скобки:
2.4. Сокращаем дробь на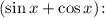
Тождество доказано.
ответ: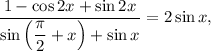 если
если 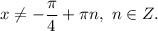
Пометка. Пункт под нахождением области допустимых значений не является обязательным при доказательстве тождества.