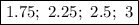Обчислити f`(4) , якщо f(x)=√x
Желательно с полным развязыванием

Показать ответ

Ответ:

aydawgva

21.05.2021 13:41

Объяснение:

1) 5/(x²+2x+1) -2/(1-x²)=1/(x-1)

5/(x+1)² +2/((x-1)(x+1)) -1/(x-1)=0

(5(x-1)+2(x+1)-(x+1)²)/((x-1)(x²+2x+1))=0

x-1≠0; x₁≠1

x²+2x+1≠0

Допустим:

x²+2x+1=0; D=4-4=0

x₂=-2/2=-1⇒x₂≠-1

5(x-1)+2(x+1)-(x+1)²=0

5x-5+2x+2-x²-2x-1=0

-x²+5x-4=0

x²-5x+4=0; D=25-16=9

x₃=(5-3)/2=2/2=1 - этот корень не подойдет для этого уравнения, так как x₁≠1.

x₄=(5+3)/2=8/2=4

ответ: 4.

2) 3/(x²-6x+9) +6/(9-x²)=1/(x+3)

3/(x-3)² -6/((x-3)(x+3)) -1/(x+3)=0

(3(x+3)-6(x-3)-(x-3)²)/((x+3)(x²-6x+9))=0

x+3≠0; x₁≠-3

x²-6x+9≠0

Допустим:

x²-6x+9=0; D=36-36=0

x₂=6/2=3⇒x₂≠3

3(x+3)-6(x-3)-(x-3)²=0

3x+9-6x+18-x²+6x-9=0

-x²+3x+18=0

x²-3x-18=0; D=9+72=81

x₃=(3-9)/2=-6/2=-3 - этот корень не подойдет для этого уравнения, так как x₁≠-3.

x₄=(3+9)/2=12/2=6

ответ: 6.

0,0(0 оценок)

Ответ:

jadeholden451

26.01.2023 16:31

Задачу можно понимать 2 разными по итогу решим оба варианта)

1-ый вариант, когда каждый раз прибавляется дробная часть исходного числа.

2-ой вариант, когда прибавляется дробная часть последнего полученного числа.

Решаем по 1-ому варианту.

Представим число как сумму целой и дробной части $x=[x]+\{x\}$

, так вот, дробной части у нас аж 3, так как Петя два раза её прибавляет

Тогда получается такое равенство: $[x]+3\{x\}=3; \ [x] \in \mathbb{N}$

Нулевой икс в целой части нет смысла рассматривать, так как дробная часть ограничена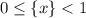 $0\leq\{x\}$

Учитываем, что целая часть числа целая, значит, и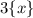 $3\{x\}$ - число тоже целое. Это возможно только в том случае, если 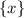$\{x\}$ или просто целое число (1 не может быть, только 0) или дробь со знаменателем 3, то есть рассматриваем

$\displaystyle 1) \{x\}=0 \Rightarrow [x]=3-3\{x\}=3 \Rightarrow x=3 \\ 2) \{x\}=\frac{1}{3} \Rightarrow [x]=3-3\cdot \frac{1}{3}=3-1=2 \Rightarrow x=2\frac{1}{3} \\ 3) \{x\}=\frac{2}{3} \Rightarrow [x]=3-3\cdot \frac{2}{3}=3-2=1 \Rightarrow x=1\frac{2}{3}$

x=3 пойдет в любом случае, а вот остальные два дробных ответа идут только в том случае, если калькулятор поддерживает арифметику с округлениями (такие, естественно, существуют, у меня дома есть такой, инженерный, он чуть поумнее стандартного калькулятора, причем необязательно программируемый).

Соответственно, начать он с этих чисел мог с инженерного калькулятора в том числе и после некоторых дробных вычислений, так что условие задачи выполнено.

Можно, конечно, и проверить эти числа ради интереса

$\displaystyle 3+0+0=3 \\ 2\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=3 \\ 1\frac{2}{3}+\frac{2}{3}+\frac{2}{3}=3$

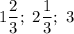
ответ: $\displaystyle 1\frac{2}{3}; \ 2\frac{1}{3}; \ 3$

Решаем по 2-му варианту.

Первое число $x=[x]+\{x\}$

Второе число $[x]+\{x\}+\{x\}=[x]+2\{x\}$

А далее все зависит от дробной части второго числа.

Если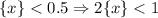 $\{x\}$ , то есть вся дробная часть прибавится и получится третье число

$[x]+2\{x\}+2\{x\}=[x]+4\{x\}$

$[x]+4\{x\}=3; \ 4\{x\} \in \mathbb{Z}; \ 0 \leq \{x\}$

Два числа получили.

Теперь рассматриваем случай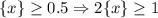 $\{x\}\geq 0.5 \Rightarrow 2\{x\}\geq 1$

То есть потенциальная дробная часть получается больше единицы, значит, необходимо эту единицу оттуда убрать и добавить к целой части, получается вот что:

$[x]+2\{x\}=[x]+1+(2\{x\}-1)$ , где в скобках дробная часть второго числа

Теперь третье число:

$[x]+1+(2\{x\}-1)+2\{x\}-1=[x]+4\{x\}-1=3 \Rightarrow \\ \Rightarrow [x]+4\{x\}=4; \ 0.5 \leq \{x\}$

Получили ещё 2 значения, их можно не проверять, но я все же напишу цепочки для достоверности:

$\displaystyle 1) \ 1.75 \xrightarrow {+0.75} 2.5 \xrightarrow {+0.5} 3; \\ 2) \ 2.25 \xrightarrow {+0.25} 2.5 \xrightarrow {+0.5} 3; \\ 3) \ 2.5 \xrightarrow {+0.5} 3 \xrightarrow {+0.0} 3; \\ 4) \ 3 \xrightarrow {+0.0} 3 \xrightarrow {+0.0} 3$