При извлечении квадратного корня или корня чётной степени ( 2n - обозначение чётного числа ) из а² (или ) надо не забыть поставить модуль, ведь сам корень чётной степени может быть только неотрицательным . А модуль любого выражения тоже неотрицателен . Причём, если выражение под модулем неотрицательно, то модуль равен самому этому выражению. Если выражение под модулем отрицательно, то модуль равен этому выражению, взятому с противоположным знаком.
Например, . Как видим, в любом
случае получаем модуль, равный неотрицательному числу .
P.S. Обратите внимание, что в 5 примере b<0 , но под модулем записан b² , который несмотря на отрицательное b всё равно будет положительным, и тогда .
В 6 примере, так как b≤0 , нечётная степень b тоже будет неположительной, тогда если .
100) Если , то .
Если , то .
Заметь, что все выражения под знаком квадратного корня или корня чётной степени неотрицательны ! И когда мы внесли под корень множители, получившиеся выражения должны быть неотрицательными .
это линейная функция вида y=kx+b, где k - коэффициент наклона прямой, значит, графики будут параллельны, если эти коэффициенты одинаковы. Например
y=3x+1 || y=3x+7 || y=3x+345 и т.д.
б) Любые линейные графики будут пересекаться, если коэффициенты наклона k будут разные. (Не будут пересекаться только, если они одинаковы, в таком случае они параллельны, как в объяснении (а).)
Например:
y=3x+1, пересекается с у=8х+10, с у=5х, у=х+7565.. и т.д.
в) О графиках можно сказать то, что они одинаковы. Это одна и та же функция
у=4х+1 и у=1+4х равны, т.к. от перестановки мест слагаемых сумма не меняется.
99) Правило:![\boxed{\ \sqrt{a^2}=|a|\ \ \ ,\ \ \ \sqrt[2n]{a^{2n}}=|a|\ }](/tpl/images/4529/9104/a373f.png) .
.
При извлечении квадратного корня или корня чётной степени ( 2n - обозначение чётного числа ) из а² (или ) надо не забыть поставить модуль, ведь сам корень чётной степени может быть только неотрицательным . А модуль любого выражения тоже неотрицателен . Причём, если выражение под модулем неотрицательно, то модуль равен самому этому выражению. Если выражение под модулем отрицательно, то модуль равен этому выражению, взятому с противоположным знаком.
) надо не забыть поставить модуль, ведь сам корень чётной степени может быть только неотрицательным . А модуль любого выражения тоже неотрицателен . Причём, если выражение под модулем неотрицательно, то модуль равен самому этому выражению. Если выражение под модулем отрицательно, то модуль равен этому выражению, взятому с противоположным знаком.
Например,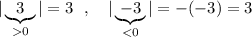 . Как видим, в любом
. Как видим, в любом
случае получаем модуль, равный неотрицательному числу .
P.S. Обратите внимание, что в 5 примере b<0 , но под модулем записан b² , который несмотря на отрицательное b всё равно будет положительным, и тогда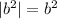 .
.
В 6 примере, так как b≤0 , нечётная степень b тоже будет неположительной, тогда если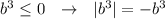 .
.
100) Если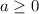 , то
, то ![a=\sqrt{a^2}\ \ ,\ \ a=\sqrt[2n]{a^{2n}}](/tpl/images/4529/9104/decbc.png) .
.
Если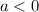 , то
, то ![a=-\sqrt{a^2}\ \ ,\ \ a=-\sqrt[2n]{a^{2n}}](/tpl/images/4529/9104/b5eb6.png) .
.
Заметь, что все выражения под знаком квадратного корня или корня чётной степени неотрицательны ! И когда мы внесли под корень множители, получившиеся выражения должны быть неотрицательными .
Например, в 6 примере:
Объяснение:
а) y=3x+1
это линейная функция вида y=kx+b, где k - коэффициент наклона прямой, значит, графики будут параллельны, если эти коэффициенты одинаковы. Например
y=3x+1 || y=3x+7 || y=3x+345 и т.д.
б) Любые линейные графики будут пересекаться, если коэффициенты наклона k будут разные. (Не будут пересекаться только, если они одинаковы, в таком случае они параллельны, как в объяснении (а).)
Например:
y=3x+1, пересекается с у=8х+10, с у=5х, у=х+7565.. и т.д.
в) О графиках можно сказать то, что они одинаковы. Это одна и та же функция
у=4х+1 и у=1+4х равны, т.к. от перестановки мест слагаемых сумма не меняется.