Степень числа, это произведение множителей, каждый из которых величиной , раз подряд, где
Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого числа вычитают показатель степени делителя:
Где - любые натуральные числа, с условием, что .
Запишем наш пример:
Для наглядности решения данный пример можно разделить на три части, и согласно свойству частного степеней, которое я записал выше можно было проще решить данный пример.
Первой частью будут известные числа:
(1)
Теперь запишем отдельно деление переменной :
(2)
Далее запишем переменную :
(3)
Так как по определению отрицательной степени:
Теперь совместим (1), (2) и (3):
- в дальнейшем данную дробь сократить невозможно, это и будет ответ.
Перепишем уравнение в виде x*y'+y-1=0 или - по сокращению на x - в виде y'+y/x-1/x=0. Это ЛДУ 1-го порядка, его решение будем искать в виде y=u*v, где u=u(x) и v=v(x) - неизвестные пока функции. Тогда y'=u'*v+u*v' и уравнение принимает вид u'*v+u*v'+u*v/x-1/x=0. Переписываем его в виде v*(u'+u/x)+u*v'-1/x=0. Так как одной из функций u или v мы можем распорядиться по произволу, то полагаем u'+u/x=0, или du/dx=-u/x. Отсюда du/u=-dx/x. Интегрируя обе части, находим ∫du/u=-∫dx/x, или ln/u/=-ln/x/, откуда u=1/x. Подставляя это выражение в уравнение, получаем уравнение v'/x-1/x=0, или v'=dv/dx=1. Отсюда dv=dx, а интегрируя это равенство, находим ∫dv=∫dx, откуда v=x+C. Тогда y=1/x*(x+C)=C/x+1. Проверка: y'=-C/x², x*y'=-C/x, 1-y=1-C/x-1=-C/x, -C/x=-C/x. ответ: y(x)=C/x+1.
Объяснение:
Степень числа, это произведение множителей, каждый из которых величиной ,
, 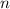 раз подряд, где
раз подряд, где
Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого числа вычитают показатель степени делителя:
Где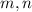 - любые натуральные числа, с условием, что
- любые натуральные числа, с условием, что  .
.
Запишем наш пример:
Для наглядности решения данный пример можно разделить на три части, и согласно свойству частного степеней, которое я записал выше можно было проще решить данный пример.
Первой частью будут известные числа:
Теперь запишем отдельно деление переменной :
:
Далее запишем переменную :
:
Так как по определению отрицательной степени:
Теперь совместим (1), (2) и (3):