Производная 2 порядка - это производная 1 порядка от производной 1 порядка: .
1. (хⁿ)'=n*xⁿ⁻¹
y''=(y')'
y'=(2x⁻³ -x²+7x-4)'=-2*3x⁻⁴-2x+7=-6x⁻⁴-2x+7;
y''=(-6x⁻⁴-2x+7)'=24/x⁵-2;
2. (u*v)'=u'v+uv'
f'(x)=(-3x*㏑x)=-3*㏑x-3x/x=-3*㏑x-3;
f''(x)=(-3*㏑x-3)'=-3/x; производная константы равна нулю.
Производная 2 порядка - это производная 1 порядка от производной 1 порядка: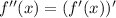 .
.
1. (хⁿ)'=n*xⁿ⁻¹
y''=(y')'
y'=(2x⁻³ -x²+7x-4)'=-2*3x⁻⁴-2x+7=-6x⁻⁴-2x+7;
y''=(-6x⁻⁴-2x+7)'=24/x⁵-2;
2. (u*v)'=u'v+uv'
f'(x)=(-3x*㏑x)=-3*㏑x-3x/x=-3*㏑x-3;
f''(x)=(-3*㏑x-3)'=-3/x; производная константы равна нулю.