Есть свойство о соотношении углов и сторон тр-ка: против большего угла лежит большая сторона и против меньшего угла лежит меньший угол, соответственно против большей стороны лежит больший и против меньшей стороны лежит меньший угол.
Т.е. нам дан △ABC, в котором дано следующее неравенство углов: . Соответственно, если сторона AC - наибольшая, то ∠B - наибольший, т.к. по свойству он лежит против большей стороны AC.
Такая же история получается и с меньшим углом △ABC. Т.е. поскольку сторона AB - наименьшая, то напротив лежащий ∠C - наименьший опять-таки по свойству. Ну и соответственно ∠A посередине.
График функции является параболой.
Основные точки параболы обозначим как: точка А - вершина параболы; B и С - точки пересечения с осью X; D - точка пересечения с осью Y.
Точка А - вершина параболы:
Вершина по оси x параболы по формуле -b/2a: -8/2=-4
Вершина по оси y подстановкой x: 16-32+7= -9
Координаты А(-4;-9)
Точки В и С - пересечение c осью X
Очевидно, что раз точки лежат на оси X, то координата y равна 0, поэтому решаем квадратное уравнение. По теореме Виета корни: -1 и -7.
Следовательно, координаты B(-1;0) и C(-7;0)
Точка D - пересечение с осью Y
Аналогично нахождению точек B и С, координата x равна 0. Подставим в функцию и найдём координату y: 0+0+7=7
Координаты D(0;7)
Для наглядности прикрепляю к ответу график функции.
Есть свойство о соотношении углов и сторон тр-ка: против большего угла лежит большая сторона и против меньшего угла лежит меньший угол, соответственно против большей стороны лежит больший и против меньшей стороны лежит меньший угол.
Т.е. нам дан △ABC, в котором дано следующее неравенство углов: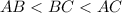
. Соответственно, если сторона AC - наибольшая, то ∠B - наибольший, т.к. по свойству он лежит против большей стороны AC.
Такая же история получается и с меньшим углом △ABC. Т.е. поскольку сторона AB - наименьшая, то напротив лежащий ∠C - наименьший опять-таки по свойству. Ну и соответственно ∠A посередине.
ответ: