очень подробно написать! Два тела, связанные невесомой нерастяжимой нитью, перекинутой через невесомый неподвижный блок движутся с ускорениями, модули которых 4,5 м\с². Коэффициент трения между телом массой m₁ и горизонтальной поверхностью 0.65. Определите массу первого тела, если масса второго 360 г.
Приравнять к нулю и решить как квадратное уравнение:
х² + 6х + 9 = 0
D=b²-4ac =36 - 36 = 0 √D=0
х=(-b±√D)/2a
х = (-6±0)/2
х = -3.
Уравнение имеет одно решение, х = -3, график данного уравнения "стоит" на оси Ох, точек пересечения с осью Ох нет.
Значит, весь график выше оси Ох, то есть, у > 0, как в неравенстве при любом значении х.
Решение неравенства: х∈(-∞; +∞).
2) х² + х - 12 < 0
Приравнять к нулю и решить как квадратное уравнение:
х² + х - 12 = 0
D=b²-4ac = 1 + 48 = 49 √D= 7
х₁=(-b-√D)/2a
х₁=(-1-7)/2
х₁= -8/2
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-1+7)/2
х₂=6/2
х₂=3.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х = -4 и х = 3, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у > 0 (график выше оси Ох)
Объяснение:
1. "Выберите в выражении 5с - (25 - 12 + 4) - а коэффициент"
Выберите один ответ:
a. 25
b. 4
c. 12
d. 5
2. Запишите частное b8 : b3 в виде степени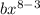
Выберите один ответ:
a. b11
b. b24
c. b5
d. b4
3. Корнем уравнения 12 - 0,8у = 26 + 0,6у является:
12 - 26 = 0.6y + 0.8y = 1.4y
y = - 14 / 1.4 = - 10
Выберите один ответ:
a. -2
b. -10
c. 1
d. -1
4. Найдите сумму многочленов 2x3 + x - 1 и x2 - 3x
2x3 + x - 1 + x2 - 3x = 2x3 + x2 - 2x - 1
Выберите один ответ:
a. 3x2 - 2x + 1
b. 2x3 - 4x + x2 - 1
c. x3 - 2x - 1
d. 2x3 + x2 - 2x - 1
5. Раскройте скобки в выражении a(c - 3) - c(a - 4) и упростите его
a(c - 3) - c(a - 4) = ac - 3a - ac + 4c = - 3a + 4c
Выберите один ответ:
a. 3a + 2ac - 4c
b. 3a + 4c
c. -3a + 4c
d. -3a - 2ac - 4c
6. Решите уравнение: 5,3х + 7,8 = -4,7х - 7,8
10x = -2*7.8 = - 15.6; x = - 1.56
Выберите один ответ:
a. -26
b. . -1,56
d. 1,52
7. Запишите произведение в виде степени: a · a · a · a = a^4
Выберите один ответ:
a. 4
b. a4
c. 4a
d. a3
8. Выберите верное равенство.
Выберите один или несколько ответов:
a. 35 + 12 = 50 - 2
b. 2 · 5 = 2 + 7
c. 12 - 8 = 9 - 3
d. 24 + 3 = 20 + 7
9. Найдите 3% от 240
Выберите один ответ:
a. 80
b. 7,2
c. 0,03
d. 8
10. Найдите разность многочленов -5y2 - 9 и 7y2- y + 1
-5y2 - 9 -( 7y2- y + 1) = - 5y2 - 9 - 7y2+ y - 1 = - 12y2 +y - 10
Выберите один ответ:
a. -12y2 + y - 8
b. -13y2 - 10
c. -12y2 + y - 10
d. 2y2 - y - 8
11. Решите уравнение: -5х - 3 = -13
-5x = -10; x = 2
Выберите один ответ:
a. 2
b. -3,2
c. -2
d. 3,2
12. Представьте выражение 3xy · (-4xy2z) = -12x^2y^3z в виде одночлена стандартного вида
Выберите один ответ:
a. -12x2y2z
b. -12x2y3z
c. -12xy2z
d. -12xy
13. "Чему будет равно выражение y ∙ y ∙ y3 ∙ y2 =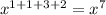 ?"
?"
Выберите один ответ:
a. y7
b. y6
c. y8
d. y5
14. Выберите числовое выражение.
Выберите один ответ:
a. 45а - 5
b. 12-
c. 23,12
d. 12 - 4 + 5
15. Какая из точек А(3;-3) и В(1;5) принадлежит графику функции у = -4х + 9
А(3;-3) у = -4*3 + 9 = -12 + 9 = - 3 ∈
В(1;5) y = - 4 * 1 + 9 = -4 + 9 = 5 ∈
Выберите один ответ:
a. А и В
b. только В
c. только А
d. ни одна
16. Как будет выглядеть в виде выражения: частное от деления суммы чисел 37 и 19 на 8?
Выберите один ответ:
a. (37 + 19) : 8
b. (19 + 8) : 37
c. 37 + 19 : 8
d. (37 + 8) : 19
В решении.
Объяснение:
Розв'яжіть квадратні нерівності :
1) х²+6х+9>0
Приравнять к нулю и решить как квадратное уравнение:
х² + 6х + 9 = 0
D=b²-4ac =36 - 36 = 0 √D=0
х=(-b±√D)/2a
х = (-6±0)/2
х = -3.
Уравнение имеет одно решение, х = -3, график данного уравнения "стоит" на оси Ох, точек пересечения с осью Ох нет.
Значит, весь график выше оси Ох, то есть, у > 0, как в неравенстве при любом значении х.
Решение неравенства: х∈(-∞; +∞).
2) х² + х - 12 < 0
Приравнять к нулю и решить как квадратное уравнение:
х² + х - 12 = 0
D=b²-4ac = 1 + 48 = 49 √D= 7
х₁=(-b-√D)/2a
х₁=(-1-7)/2
х₁= -8/2
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-1+7)/2
х₂=6/2
х₂=3.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х = -4 и х = 3, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у > 0 (график выше оси Ох)
при х∈(-∞; -4)∪(3; +∞).
Неравенство строгое, скобки круглые.
Решение неравенства х∈(-∞; -4)∪(3; +∞).