Согласно теорему Безу, значение многочлена в точке равно остатку от деления многочлена на .
Так как мы знаем, что -4 -- корень уравнения, то остаток от деления многочлена на равен 0. Запишем получившееся равенство:
.
Получили, что наш многочлен равняется .
Далее, для того, чтобы найти второй корень уравнения, можно поделить многочлен на в столбик, можно использовать теорему Виета, можно просто решить через дискриминант.
Как бы Вы не решали, многочлен раскладывается следующим образом:
Объяснение:
Согласно теорему Безу, значение многочлена в точке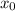 равно остатку от деления многочлена на
равно остатку от деления многочлена на  .
.
Так как мы знаем, что -4 -- корень уравнения, то остаток от деления многочлена на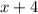 равен 0. Запишем получившееся равенство:
равен 0. Запишем получившееся равенство:
Получили, что наш многочлен равняется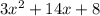 .
.
Далее, для того, чтобы найти второй корень уравнения, можно поделить многочлен на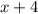 в столбик, можно использовать теорему Виета, можно просто решить через дискриминант.
в столбик, можно использовать теорему Виета, можно просто решить через дискриминант.
Как бы Вы не решали, многочлен раскладывается следующим образом:
Значит второй корень: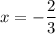
3х²+14х+с=0
х₁=-4, найдем х₂ и с.
Подставим первый корень в уравнение, получим 3*16+14*(-4)+с=0, откуда
48-56=-с, т.о., с =8
ПО теореме Виета х₁*х₂=8/3⇒х₂=(8/3):(-4)=-2/3
ОТВЕТ с =8; х₂=-2/3