Огромное ! решить при составления уравнений ( такие скобочки ), на фотопример: пусть х руб стоит карандаш, тогда у руб стоит тетрадь.составляем систему уравнений: { 3у+2х=77 2у+6х=84|: 2 я в этот ничего не понимаю!
Мы делаем предположение, что то, что нам дано неверно, к примеру:
Доказать иррациональность числа
Допускаем противное, что число - рациональное, после чего уже доказываем что наше предположение не верно, в примере с корнем:
Любое рациональное число можно представить как несократимую дробь, где числитель - целое число, а знаменатель - натуральное
Отсюда следует, что чётно, значит, чётно и a; следовательно, делится на 4, а значит, и тоже чётны. Полученное утверждение противоречит несократимости дроби . Это противоречит изначальному предположению и - иррациональное число.
А) Первая бригада за шесть дней выполняет всё задание; значит, за один день она выполнит 1/6 часть задания.
Вторая бригада за десять дней выполняет всё задание; значит, за один день она выполнит 1/10 часть задания.
За 4 дня первая бригада выполнит 1/6 * 4= 4/6=2/3 часть задания.
За 3 дня вторая бригада выполнит
1/10 * 3=3/10 часть задания.
Работая 7 дней раздельно они выполнят
2/3 + 3/10=(2*10+3*3)/3*10=29/30 часть задания. Значит, всё задание выполнено не будет (1/30 часть задания сделано не будет).
Б) первая бригада за 1 день делает
1/6 часть задания; вторая бригада за 1 день делает 1/10 часть задания;
вместе за 1 день делают
1/6 + 1/10=(10+6)/6*10=16/60=4/15 часть задания;
а всё задание вместе сделают за
1 : 4/15=15/4 дня; в день они работают по 8 часов (48:6=8; 80:10=8); значит всё задание вместе они сделают за 15/4 * 8=15*2=30 часов.
ЕСЛИ НЕ СЛОЖНО ТО ОТМЕТЬ, КАК ЛУЧШИЙ ОТВЕТ
Мы делаем предположение, что то, что нам дано неверно, к примеру:
Доказать иррациональность числа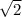
Допускаем противное, что число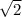 - рациональное, после чего уже доказываем что наше предположение не верно, в примере с корнем:
- рациональное, после чего уже доказываем что наше предположение не верно, в примере с корнем:
Любое рациональное число можно представить как несократимую дробь, где числитель - целое число, а знаменатель - натуральное
Отсюда следует, что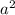 чётно, значит, чётно и a; следовательно,
чётно, значит, чётно и a; следовательно, 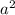 делится на 4, а значит,
делится на 4, а значит,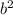 и
и 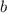 тоже чётны. Полученное утверждение противоречит несократимости дроби
тоже чётны. Полученное утверждение противоречит несократимости дроби 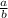 . Это противоречит изначальному предположению и
. Это противоречит изначальному предположению и 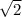 - иррациональное число.
- иррациональное число.