Определи площадь фигуры,
заданной системой неравенств :

x≤10;
y≤0;
4x+4y≥11.
ответ округлить до сотых!

Показать ответ

Ответ:

xato2003

06.11.2021 08:09

$$9x^2+\frac{25}{x^2}=226;$

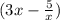
Попробуем в левой части выделить полный квадрат, как раз от выражения $(3x-\frac{5}{x})$

$$(3x)^2-2\cdot 3x\cdot \frac{5}{x} + (\frac{5}{x})^2+2\cdot 3x\cdot \frac{5}{x}=226;$

Здесь удвоенное произведение я искусственно создал для выделения квадрата, но чтобы не нарушить равенства, надо это же удвоенное произведение с противоположным знаком добавить, что и было сделано.

$$(3x-\frac{5}{x})^2+ 30=226; (3x-\frac{5}{x})^2=196=(\pm14)^2 \Rightarrow$

$$(3x-\frac{5}{x})=\pm 14$

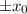Было получено два значения и не зря. Если решать уравнение из условия, то мы обязательно получим 2 корня (кроме случая x=0, на котором даже не определено второе слагаемое и потому его в расчет не берем), это $\pm x_0$ и второе выражение, которое зависит от этих корней, может и будет принимать не одно лишь значение, а 2.

ответ: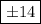 $\boxed{\pm14}$

0,0(0 оценок)

Ответ:

kairat0101

04.03.2020 03:37

1. -35x^6y^2+zx^3y^3+21x^2y^5

2. (-6x^2+9x^3)(3x^2+11x)=-18x^4-66x^3+27x^5+99x^4

3. (x+2)(x-5)-3x(1-2x)=x^2-5x+2x-10-3x+6x^2=7x^2-6x^2+10

(a+3)(a-2)+(a-3)(a+6)=a^2-2a+3a-6+a^2+6a-3a=2a^2+4a-6

(x-7)(3x-2)-(5x+1)(2x-4)=3x^2-2x-21x+14-10x^2+20x-2x+4=-7x^2-5x+18

(5x-2y)(3x+5y)-(2,5x-3y)(4x+8y)=15x^2+25xy-6xy-10y^2-10x^2-40xy+12xy+24y^2=5x^2+14y^2-11xy

(b+6)(b-6)-3b(b+2)=b^2-6b+6b-36-3b^2-6b=-2b^2-6b-36

(3a-2)(3a+2)+(a-8)(a+8)=9a^2+6a-6a-4+a^2+8a-8a-64=10a^2-4

(5x-3y)(5x+3y)+(a-8)(a+8)=25x^2+15xy-15xy-9y^2+a^2+8a-8a-64=25x^2-9y^2+a^2-64

(c-2)(3-c)-(5-c)(5+c)=3c-c^2-6+2c-25-5c+5c+c^2=5c-31

4.По аналогии с 3 - открываешь скобки и решаешь простое уравнение.

5. x^2-4x+3=x^2-x-3x+3=x(x-1)-3(x-1)=(x-3)(x-1)

6. 16^4-2^10 кратно 7 тогда, когда разница основ и сумма степеней кратна 7(делиться без остатка)

(16-2)/7=2

(10+4)/7=2, доказано .

все остальное по аналогии, удачи))

0,0(0 оценок)

Популярные вопросы: Алгебра