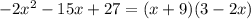5) (2x-3)(2x+3)-1=5x+(x-2)²
(4х²+6х-6х-9)-1=5х+(х²-4х+4)
Раскрываем скобки
4х²-9-1=5х+х²-4х+4
Переносим всё в левую часть
4х²-х²-5х+4х-9-1-4=0
3х²-х-14=0
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
6) y³-6y=0
Решаем уравнение методом разложения на множители
Выносим общий множитель за скобки
y(y²-6)=0
y₁=0; у²-6=0
у²=6
у₂=√6;у₃=-√6
7) 6x⁴+3,6x²=0
6х²(х²+0,6)=0
6х²=0 ⇒х=0
х²+0,6=0
х²=-0,6
Дискриминант отрицательный. Из отрицательного числа, квадратный корень не извлекается.
a)
б) Допустим
решив это уравнение мы найдём корни и сможем разложить его на множители.
соответственно
разложите на множители квадратный трехчлен:
в) Аналогично б решаем
г) По аналогии решаем и г
5) (2x-3)(2x+3)-1=5x+(x-2)²
(4х²+6х-6х-9)-1=5х+(х²-4х+4)
Раскрываем скобки
4х²-9-1=5х+х²-4х+4
Переносим всё в левую часть
4х²-х²-5х+4х-9-1-4=0
3х²-х-14=0
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
6) y³-6y=0
Решаем уравнение методом разложения на множители
Выносим общий множитель за скобки
y(y²-6)=0
y₁=0; у²-6=0
у²=6
у₂=√6;у₃=-√6
7) 6x⁴+3,6x²=0
Решаем уравнение методом разложения на множители
Выносим общий множитель за скобки
6х²(х²+0,6)=0
6х²=0 ⇒х=0
х²+0,6=0
х²=-0,6
Дискриминант отрицательный. Из отрицательного числа, квадратный корень не извлекается.
a)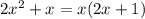
б) Допустим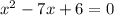
решив это уравнение мы найдём корни и сможем разложить его на множители.
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
соответственно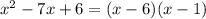
разложите на множители квадратный трехчлен:
в) Аналогично б решаем
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
соответственно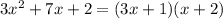
г) По аналогии решаем и г
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
соответственно