Определи, при каких значениях переменной не имеет смысла алгебраическая дробь 2−17+1(2+11)(2−11).

Дробь не имеет смысла при , равном или
(первым введи меньшее число).
ответить!

Условие. Y²+xy-4x-9y+20=0 ;   y=ax+1 ;   x>2

найти все значения а, при которых графики имеют одну общую точку(в нашем случае (ax+1)² + x(ax+1) -4x - 9(ax+1)+20=0 имеет единственное решение).

Подставим у = (ax+1)² в уравнение у²+xy-4x-9y+20=0, получим

Найдем дискриминант квадратного уравнения относительно x

Получим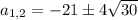

Если подставить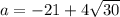 , т.е. имеется квадратное уравнение 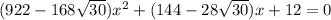, у которого корень

Если подставить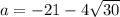 , т.е. имеется квадратное уравнение 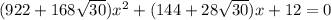, у которого корень

ответ: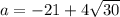

Объяснение:

1) проверим для n=3

2³=8 ; 2*3+1=7 ; 2³>2*3+1 верно (1)

2) предположим что неравенство верно при n=k (k>3) (2)

3) при n=k+1 проверим выполнение неравенства

2^(k+1)=2*2^k

2(k+1)+1=2k+3

по предположению (2)  2^k>2k+1

умножим обе части на 2

2*2^k>2(2k+1)=4k+2

2*2^k>4k+2

сравним 4k+2 и 2k+3  для этого определим знак их разности

4k+2 - (2k+3)=4k+2-2k-3=2k-3 так как k>3 то 2k>2*3=6

2k>6 и тем более 2k>3 ⇒ 2k-3>0 ⇒ 4k+2 - (2k+3)>0 ⇒ 4k+2 > (2k+3)  

так как 2^(k+1)>4+2k  и 4+2k>2k+3 и 2k+3=2(k+1)+1

то   2^(k+1)> 2(k+1)+1  то есть неравенство выполняется для n=k+1    (3)

из (1); (2); (3) ⇒ неравенство верно для любого n>3