Необязательно решать неравенство, чтобы ответить на вопрос задачи.
Преобразуем неравенство к виду:
Когда неравенство выполнится? Когда два слагаемых будут точно положительны, а это происходит, если вычитаемое в каждой скобке меньше соответствующего уменьшаемого. То есть справедлива следующая система неравенств:
Значит, все x ∈ [-5; -2) нам точно подходят.
Теперь рассмотрим случай, когда неравенство точно не выполнится. Это случай, противоположный первому.
Значит, все x ∈ (1; 5] нам точно не подходят.
Остаётся перебрать оставшиеся x: -2; -1; 0; 1.
При x = -2 получаем
При x = -1
При x = 0
При x = 1 - не удовлетворяет условию
Следовательно, нужные нам x: -5, -4, -3, -2, -1, 0. Их сумма равна -15.
Необязательно решать неравенство, чтобы ответить на вопрос задачи.
Преобразуем неравенство к виду:
Когда неравенство выполнится? Когда два слагаемых будут точно положительны, а это происходит, если вычитаемое в каждой скобке меньше соответствующего уменьшаемого. То есть справедлива следующая система неравенств:
Значит, все x ∈ [-5; -2) нам точно подходят.
Теперь рассмотрим случай, когда неравенство точно не выполнится. Это случай, противоположный первому.
Значит, все x ∈ (1; 5] нам точно не подходят.
Остаётся перебрать оставшиеся x: -2; -1; 0; 1.
При x = -2 получаем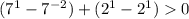
При x = -1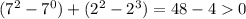
При x = 0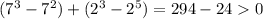
При x = 1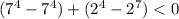
- не удовлетворяет условию
Следовательно, нужные нам x: -5, -4, -3, -2, -1, 0. Их сумма равна -15.
ответ: -15
task/29729177 Решить уравнение ctg(2x) - ctg(x) = 2ctg(4x)
ОДЗ : { sin2x ≠ 0 ; sinx ≠ 0 ; sin4x ≠0 . x ≠ πk/4 , k ∈ ℤ .
ctg(2x) - ctg(x) = 2ctg(4x) ⇔ ctg(2x) - 2ctg(4x) = ctg(x) ⇔
ctg(2x) -(ctg²(2x)-1) /ctg2x =ctg(x) ⇔1/ctg(2x)=ctg(x)⇔2ctgx / (ctg²x -1) =ctgx⇔
|| ctgx ≠ 0 || 2 / (ctg²x -1) = 1 ⇔ 2 = ctg²x - 1 ⇔ ctg²x = 3 ⇔ || ctgx = ±√3 ||
(1+cos2x) / (1-cos2x) = 3 ⇔ 1+cos2x =3 - 3cos2x ⇔ cos2x = 1/2 ⇔
2x = ± π/3 + 2πk , k ∈ ℤ .
ответ: x =± π/6 + πk , k ∈ ℤ