Пусть сторона квадрата равна . Тогда по условию, Теперь попробуем найти стороны треугольника PQD:
1) найти PD:
По теореме Пифагора
2) найти PQ и QD:
Проведем прямую проходящую через точку Q и параллельную BC, и отметим точки пересечения с квадратом ABCD как M и N где M∈AB, N∈CD и прямую проходящую через точку Q и параллельную AB, пересекающую квадрат в точках E и F где E∈BC, F∈AD.
Тогда из параллельности PQ||BC, FQ||CD и свойства пропорциональных отрезков получаем,
Следовательно из ,
Также из-за того, что AP<AM,
Заметим что, AMQF - прямоугольник, тогда
Теперь нам известны катеты прямоугольных треугольников PMQ и QFD, значит мы можем найти и их гипотенузы PQ и QD,
3) доказать что ∠PQD=90°:
Действительно,
Из обратной теоремы Пифагора следует что, ∠PQD - прямой угол.
4) доказать что ∠PQD - наибольший угол соответствующего треугольника:
Предположим обратное, допустим в треугольнике PQD есть угол больший 90°, но тогда сумма углов этого треугольника будет больше 180° - противоречие.
По итогу имеем то что, ∠PQD=90° - наибольший угол треугольника PQD.
Лодка, плывущая по течению, до места встречи пройдёт 46,8 км
Лодка, плывущая против течению, до места встречи пройдёт 37,2 км
Объяснение:
Пусть скорость лодок в стоячей воде х км/ч. Тогда скорость по течению (х+4) км/ч, а против течения (х-4) км/ч Т.к. лодки плыли 1,2 ч. То можно составить и решить уравнение
1,2 (х-4) +1,2 (х+4) = 84
1,2(х-4+х+4)= 84
1,2*2*х= 84
х= 84/2,4
х=35
Скорость лодки в стоячей воде равна 35 км/ч.
Лодка, плывущая по течению, до места встречи пройдёт
1,2 (35+4)= 46,8 км
Лодка, плывущая против течению, до места встречи пройдёт
90 градусов.
Объяснение:
Пусть сторона квадрата равна
. Тогда по условию,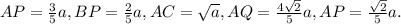 
Теперь попробуем найти стороны треугольника PQD:
1) найти PD:
По теореме Пифагора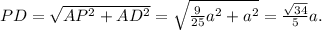
2) найти PQ и QD:
Проведем прямую проходящую через точку Q и параллельную BC, и отметим точки пересечения с квадратом ABCD как M и N где M∈AB, N∈CD и прямую проходящую через точку Q и параллельную AB, пересекающую квадрат в точках E и F где E∈BC, F∈AD.
Тогда из параллельности PQ||BC, FQ||CD и свойства пропорциональных отрезков получаем,
Следовательно из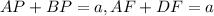
,
Также из-за того, что AP<AM,
Заметим что, AMQF - прямоугольник, тогда
Теперь нам известны катеты прямоугольных треугольников PMQ и QFD, значит мы можем найти и их гипотенузы PQ и QD,
3) доказать что ∠PQD=90°:
Действительно,
Из обратной теоремы Пифагора следует что, ∠PQD - прямой угол.
4) доказать что ∠PQD - наибольший угол соответствующего треугольника:
Предположим обратное, допустим в треугольнике PQD есть угол больший 90°, но тогда сумма углов этого треугольника будет больше 180° - противоречие.
По итогу имеем то что, ∠PQD=90° - наибольший угол треугольника PQD.
Скорость лодки в стоячей воде равна 35 км/ч.
Лодка, плывущая по течению, до места встречи пройдёт 46,8 км
Лодка, плывущая против течению, до места встречи пройдёт 37,2 км
Объяснение:
Пусть скорость лодок в стоячей воде х км/ч. Тогда скорость по течению (х+4) км/ч, а против течения (х-4) км/ч Т.к. лодки плыли 1,2 ч. То можно составить и решить уравнение
1,2 (х-4) +1,2 (х+4) = 84
1,2(х-4+х+4)= 84
1,2*2*х= 84
х= 84/2,4
х=35
Скорость лодки в стоячей воде равна 35 км/ч.
Лодка, плывущая по течению, до места встречи пройдёт
1,2 (35+4)= 46,8 км
Лодка, плывущая против течению, до места встречи пройдёт
1,2 (35-4)= 37,2 км